Uncertainty analysis in IEHIAS

The text on this page is taken from an equivalent page of the IEHIAS-project.

Assessing complex policy problems such as those that are the target of integrated environmental health impact assessments inevitable involves major uncertainties. Doing an assessment without considering these uncertainties is a pointless task; likewise, presenting the results of an assessment without giving information about the uncertainties involved makes the information more-or-less meaningless. Ideally, uncertainties are tracked and quantified throughout the execution phase in order to control them, and ensure that the assessment does not become too uncertain to be of value (see Managing uncertainties). Without exception, they need to be evaluated by the end of the process and presented as part of the final assessment results.

The dimensions of uncertainty

Uncertainties arise at every step in an assessment: from the initial formulation of the question to be addressed to the ultimate reporting and interpretation of the findings. They also take many different forms, and are not always immediately obvious. It is therefore helpful to apply a clear and consistent framework for identifying and classifying uncertainties, in order to ensure that key sources of uncertainty are not missed and that users can understand how they arise and what their implications might be. In particular, it is useful to distinguish between three essential properties of uncertainty:

• location - where within the causal chain it arises
• nature - its source or cause and manner of representation
• level - its magnitude or degree of importance

Describing uncertainties

Uncertainties can be described either quantitatively or qualitatively, and in each case using different metrics and methods. Which is appropriate depends on the nature of the issue being assessed and the methods being used, as well as the purpose of the assessment. In general, quantitative methods are more useful to enable comparisons between different policy options and inform decision-making; in some circumstances, however, qualitative methods may have to be used because of the limitations of the data. Many users may also find qualitative measures more easy to understand: often, therefore, both need to be presented.

Framework for uncertainty classification

Uncertainty: any departure from the unachievable ideal of complete deterministic knowledge of the system. From the risk assessors point of view, uncertainty is best thought of as a two dimensional concept, including the i) Location, and ii) Level of uncertainty.

Location of uncertainty: refers to the aspect of the risk assessment model that is characterized by uncertainty. All of the widely used approaches to risk assessment rely on methodologies that can be considered models - that is, abstractions of the real world issues under consideration.

Example 1. Location of uncertainty

Consider a map of the world that was drawn by a European cartographer in the 15th century. Such a map would probably contain a fairly accurate description of the geography of Europe. Because the trade of spices and other goods between Europe and Asia was well established at that time, one might expect that those portions of the map depicting China, India, central Asia and the middle-east were also fairly accurate. However, as Columbus only ventured to America in 1492, the portions of the map depicting the American continent would likely be quite inaccurate (if they existed at all). Thus, it would be possible to point to the American continent as a “location” in the model that is subject to large uncertainty. In this case, the model in question is a map of the world, and all locations are geographic components of the map.

Generic model locations: The description of the model locations will vary according to the assessment method (model) that is in use. Nonetheless, it is possible to identify certain categories of locations that apply to most models. These are:

• Context
• Model structure
• Inputs
• Parameters
  • Exact parameters (e.g. π and e);
  • Fixed parameters, (e.g. the gravitational constant g); and
  • A priori chosen or calibrated parameters.

The uncertainty on exact and fixed parameters can generally be considered as negligible within the analysis. However, the extrapolation of parameter values from a priori experience does lead to parameter uncertainty, as past circumstances are rarely identical to current and future circumstances. Similarly, because calibrated parameters must be determined by calibration using historical data series and sufficient calibration data may not be available and/or errors may be present in the data that is available, calibrated parameters are also subject to parameter uncertainty.

Model outcome (result)

Level of uncertainty: refers to the degree to which the object of study is uncertain, from the point of view of the decision maker. A continuum of different levels of uncertainty includes:

• Determinism
• Statistical uncertainty
• Scenario uncertainty

Example 2: scenario uncertainty

Consider the case antimicrobials and antibiotics in animal feedstuff. Antibiotics are probably the single most important discovery in the history of medicine. They have saved millions of lives by killing bacteria that cause diseases in humans and animals. Beginning in the 1940s, low levels of antibiotics began to be added to animal feedstuff as it was observed that this practice could increase the growth rate of the animals, increase the efficiency of food conversion by the animals, as well as have other benefits such as improved egg production in laying hens, increased litter size in sows and increased milk yield in dairy cows. Over the years, concerns developed over the potential for bacteria to develop resistance to the antibiotics. It was feared that the widespread use of the antibiotics would lead to the development of resistant bacterial strains, and that these antibiotics would therefore no longer be effective in the treatment of disease in humans. The scientific evidence available indicated that the development of bacterial resistance could take place, but how quickly and to what extent this could occur remain unknown to this day. The question of whether the short-term benefits outweigh the potential long-term risks is still being debated. In this case, the scenario is clear but the probability of its occurrence is unknown. The uncertainty here is of a level greater than statistical uncertainty, and is referred to as scenario uncertainty.

Recognized ignorance

Total ignorance

Example 3: ignorance

Consider the case of mad cow disease (also known as BSE) in Britain. Following the diagnosis of the first cases of BSE in 1986, it was noticed that the pathological characteristics of the new disease closely resembled scrapie, a contagious disease common in the UK sheep population. Health authorities soon observed that contaminated feed was the principle cause of BSE in cattle. However, the question remained: contaminated by what? There was no scientific evidence that eating sheep meat from scrapie-infected animals could pose a health risk, and health authorities could not be sure that the agent that caused BSE had in fact derived from scrapie. Moreover, there was no scientific evidence indicating that BSE could subsequently be transmitted to humans in the form of Creutzfeldt-Jakob disease (CJD), and it was a big surprise when, in 1995, it was discovered that this could happen.

The notion of ignorance is illustrated by considering the uncertainty characterizing an assessment of the potential costs associated to BSE, performed at the time of the discovery of BSE in 1986. No historical data on BSE was available and scientific understanding of how the disease is contracted was limited. The extent of the public outcry that would eventually occur remained unknown, as did the extent of the loss of exports and the drop in domestic demand that ensued. Data on the relationship between BSE and CJD would not become available for another 10 years. Furthermore, at the time there was not even a credible basis to claim that all of the potential ramifications or costs (outcomes) of the BSE crisis had been thought of. The uncertainty characterizing this situation is a good example of ignorance.

Methods for uncertainty analysis

Uncertainty analysis can be done in two general ways:

• quantitatively, by trying to estimate in numerical terms the magnitude of uncertainties in the final results (and if appropriate at key stages in the analysis); and
• qualitatively, by describing and/or categorising the main uncertainties inherent in the analysis.

While quantitative analysis may generally be considered superior, it suffers from number of disadvantages. In particular, not all sources of uncertainty may be quantifiable with any degree of reliability, especially those related to issue-framing or value-based judgements. Quantitative measures may therefore bias the description of uncertainty towards the more computational components of the assessment. Many users are also unfamiliar with the concepts and methods used to quantify uncertainties, making it difficult to communicate the results effectively. In many cases, therefore, qualitative measures continue to be useful either alone or in combination with quantitative analysis.

Quantitative methods

A range of methods for quantitative analysis of uncertainty have been deveoped. These vary in their complexity but all have the capability to represent uncertainty at each stage in the analysis and to show how uncertainties propagate throughout the analytical chain. Techniques include: sensitivity analysis, Taylor Series Approximation (mathematical approximation), Monte Carlo sampling (simulation approach) and Bayesian statistical modeling.

1. Sensitivity analysis. This assesses how changing inputs to a model or an analysis can affect the results. It is undertaken by repeatedly rerunning the analysis, incrementally changing target variables on each occasion, either one at a time or in combination It thus allows the relative effects of different parameters to be identified and assessed. It is especially useful for analysing the assumptions made in assessment scenarios (e.g. by changing the emissions or to explote best and worst case situations). The main limitation of sensitivity analysis is that it becomes extremely complex if uncertainties arise through interactions between a large number of variables, because of the large number of permutations that might need to be considered.
2. Taylor Series Approximation. This is a mathematical technique to approximate the underlying distribution that characterises uncertainty in a process. Once such an approximation is found, it is computationally inexpensive and so is useful when dealing with large and complex models for which more sophisticated methods may be infeasible.
3. Monte Carlo simulation. This is a reiterative process of analysis, which uses repeated samples from probability distributions as the inputs for models. It thus generates a distribution of outputs which reflects the uncertainties in the models. Monte Carlo simulation is a very useful technique when the assessment concerns the probability of exceeding a specified (e.g. safe) limit, or where models are highly non-linear, but it can be computationally expensive.
4. Bayesian statistical modeling. The preceding approaches all apply to deterministic models. In practice, many of the parameters in these models have been estimated from data but are then, at least initially, treated as known and fixed entities in the models. Stochastic models estimate the parameters from the data and fit the model in one step, thereby directly incorporating uncertainty in the parameter estimates due to imperfections in the data. Bayesian modelling goes one step further and incorporates additional uncertainty in the parameters from other sources (expressed in terms of probability distributions).

Further details on these quantitative approaches to assessing uncertainty can be found in the Toolkit section of this Toolbox. A number of computational packages are also listed below, which provide the capability to apply these techniques.

Qualitative methods

By their nature, qualitative methods of uncertainty analysis tend to be less formalised than quantitative methods. On the one hand this is a significant disadvantage, for it means that results are not always easy to compare between different studies or analysts; on the other hand, it makes these approaches far more flexible and adaptable to circumstance. As a result, qualitative methods can be devised according to need, so that they may be used to evaluate almost any aspect of uncertainty, at any stage in the analysis, in almost any context.

To be informative, however, qualitative methods must meet a number of criteria:

1. they must be based on a clear conceptual framework of uncertainty, and clear criteria;
2. they must be (at least internally) reproducible - i.e. would generate the same results whenapplied to the same information in the same context;
3. they must be interpretable for the end-users - i.e. they should be expressed in terms that are both familiar and meaningful to the end-user;
4. they should focus on uncertainties in the assessment that influence the utility of the results and/or might affect the decisions that might be made as a consequence.

A number of techniques can be used in this context. A very useful approach is to employ simple, relative measures of uncertainty, expressed in terms of 'the degree of confidence'. One example of this is the IPCC (2005) system, sumarised in Table 1 below. This can be applied to each step in the assessment (and each of the main models or outcomes), in order to show where within the analysis the main uncertainties lie. Ideally, estimates of confidence are made not by a single individual, but by a panel of assessors, who are either involved in the assessment, or provided with relevant details of, the assumptions made and the data sources and procedures used.

Table 1. The IPCC level of confidence scale

Level of confidence	Degree of confidence in being correct
Very high	At least 9 out of 10 chance
High	About 8 out of 10
Medium	About 5 out of 10
Low	About 2 out of 10
Very low	Less than 1 out of 10

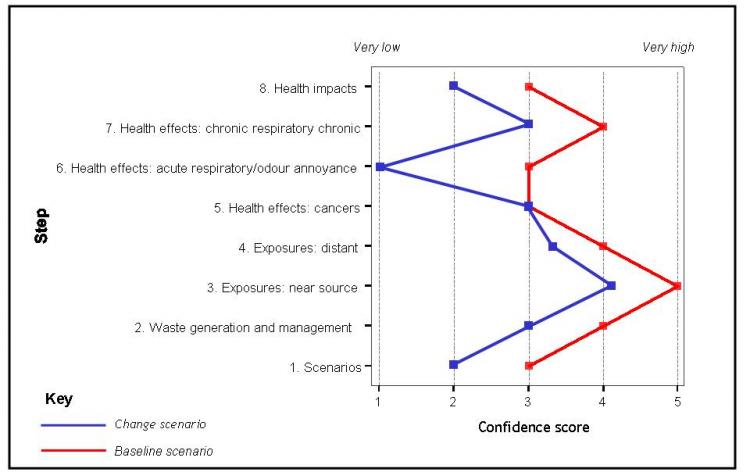
Results of using a scorecard such as this can be reported textually. For the purpose of communication, however, scales of this type can usefully be represented diagrammatically in the form of an 'uncertainty profile' (see example below), showing the level of confidence in the outcomes from each stage in the analysis. This helps to show how uncertainties may both propagate and dissipate through the analysis, and enables comparison between different pathways, scenarios or assessment methods.

Figure 1. Example of an uncertainty profile for assessment of health effects of waste management under two policy scenarios

Value of information

Value of information (VOI) analysis is "…a decision analytic technique that explicitly evaluates the benefits of collecting additional information to reduce or eliminate uncertainty" (Yokota and Thompson 2004a). As such, it covers a number of different approaches with different requirements and objectives.

To be able to perform a value of information analysis, the researcher needs to define possible decision options, consequences of each option, and the uncertainty of each input variable. With the VOI method, the researcher can then estimate the effect of additional information to decision making and guide the further development of the analytical model(s) that underpin the assessment.

This review outlies different VOI methods, requirements of the analysis, mathematical background and applications. It concludes with a short summary of the previously published VOI reviews by Yokota and Thompson (2004a, 2004b). A link to further information is also included under See also, below.

A family of analyses

The term value of information analysis covers a number of different decision analyses.

Expected value of perfect information (EVPI) analysis estimates the value of completely eliminating uncertainty from a specified decision. EVPI analysis does not consider the sources of uncertainty, but only how much the decision would benefit if uncertainty were removed. The VOI of a particular input variable (X) can be analysed with expected value of perfect X information (EVPXI) (or expected value of partial perfect information (EVPPI) analysis. The sum of all individual EVPXIs from all input variables is always less than EVPI.

The situations where uncertainty of the decision could be reduced to zero are exceptional, especially in the field of environmental health. Therefore, the results of EVPI and EVPXI analyses should be treated as an indication of the maximum gain that could be achieved by reducing uncertainty. A more realistic approach is therefore provided by expected value of sample information (EVSI), or partial imperfect (ie. EVII) analysis, which estimates the gain (in terms of the quality of the decision) of reducing uncertainty of the model to a specified level. Expected value of sample X information (EVSXI) (or EVPII) does the same in relation to a particular input variable. The use of these two analyses increases requirements of the model since the targeted uncertainty level must be defined. A further method - the expected value of including uncertainty (EVIU) - evaluates the benefit of allowing for uncertainty in the decision, but is beyond the scope of this review.

Estimating the value of information

VOI analysis estimates the difference between the expected utility of the optimal decision, given new information, and the expected utility of the optimal decision given current information. Yokota and Thompson (2004b) defined the EVPI as:

where: s is the uncertain input, and f(s) represents the probability distribution representing prior belief about the likelihood of s.

The complete review of different mathematical solutions is beyond the scope of this review and thus only the EVPI is presented here. The detailed mathematical background of different VOI analyses, and the solutions used in past analyses, are given by Morgan and Henrion (1992) and Yokota and Thompson (2004b).

Setting up the analyses

To be able to perform a VOI analysis a modeller needs information on:

1. the available decision options;
2. the consequences of each option; and
3. the uncertainties and reliability of the data.

In addition to these, both gains and losses of the options must be quantified using common metrics (monetary or non-monetary).

Available decision options. The first requirement for the VOI analysis is that the available options have been defined. In the economic literature the decision is usually seen, for example, as a question of whether or not to invest. In the field of environmental health the decisions might represent choices between different control technologies or available regulations. In an ideal case, the possible options would have been explicitly defined by the authorities or the customer of the study. More often, however, the available options are defined during the assessment process; effective methods of stakeholder communication are then needed during this stage to help identify the different options. In a research context, the possible options can be defined by the modeller or the modelling team.

Consequences of each option. The second requirement is that the consequences of each possible option must be defined (e.g. the effect of a specified control technology on the emissions and, consequently, on human health). These imply the development of a causal model of the system being analysed.

Uncertainties and reliability of the data. The third requirement is that the uncertainties and reliability of the data must be made explicit in the model. Again, in the ideal case the uncertainties in the data will have been pre-defined, or the data are available in a form that enables the modeller to assess the uncertainties. In reality, the data are usually sparse, and the uncertainties must be assessed based on inadequate information - for example, from different point estimates reported in the different studies. Expert elicitation and similar methods are available to define the uncertainties. In the absence of data, uncertainties may have to be evaluated by the modeller (author judgement).

The outcomes of the actions must be quantified using a monetary or non-monetary metric. Again, in economic analyses, the common metric is by definition monetary. In the area of environmental health, metrics based on health effect (e.g. life expectancy, QALY, DALY) may be used. Inevitably, using summary measures such as these tends to increase the complexity and uncertainty of the model.

Applications for health impact assessment

In environmental health impact assessment, the main use of value of information analysis is to help identify and manage uncertainties. In this context, it provides a form of sensitivity analysis, aimed at determining:

• whether the assessment model contains explicit uncertainties, and if so in which parts;
• what are the key input parameters or assumptions in the model;
• which parts of the model need to be specified in more detailed.

All of these start from the question of whether or not model uncertainties have an effect on decision making.

VOI analysis can also be used, however, at other stages in the assessment. At the screening stage, for example, it can help to determine whether to proceed with the assessment on the basis of readily available information or to wait and collect more information. Likewise, during appraisal of the results, it can indicate whether the assessment provides a sufficient basis for action, or whether it would be more effective to delay intervention until more information as been gathered. In the economic literature, this latter role is often seen as the main contribution of VOI analysis. In the context of environmental health impact assessment, however, opportunities to seek or allocate more funding for additional research and data collection are rare, so VOI is less useful at the appraisal stage.

VOI analysis in past risk assessments

The use of value of information analysis in the medical and environmental fields has been extensively reviewed in two articles by Yokota and Thompson (2004a, 2004b).

The first review covers issues such as the use of VOI analyses in different fields, the use of different VOI analyses, and motivations behind the analyses. In this, they trace the concept of VOI back to the 1960s. The earliest applications in the medical and environmental fields date from the 1970s, but it has only been since 1985 that the use of VOI analysis spread more widely and grown more rapidly. In most of the analyses the number of uncertain input variables has been between one and four. EVPI or EVSI analyses have been the most common approaches, while EVPXI and EVSXI analyses have been relatively rare. Applications extend across a number of different fields from toxicology to water contamination studies. Yokota and Thompson (2004a) argue, however, that the published analyses show "a lack of cross-fertilization across topic areas and the tendency of articles to focus on demonstrating the usefulness of the VOI approach rather than applications to actual management decisions". This may reflect the complexity of these areas of application, and of the policy decisions that need to be made.

The second review focuses in more detail on environmental health applications and the methodological development andthe challenges that the methods face. Although the development of the personal computers has increased the analytical possibilities, a number of analytical problems still exist. More fundamental, however, are the questions of how to model decisions, how to value the outcomes and how to characterise uncertainties. In the field of environmental health impact assessment, it might be noted, identifying and modelling different decisions is probably the most challenging of these problems.

See also

Software tools

• Crystalball: a spreadsheet-based software suite for predictive modeling, forecasting, Monte Carlo simulation and optimization
• @risk: a user friendly software that works within Excel to perform Monte Carlo sampling
• Aguila: stand-alone visualization software which allows interactive exploration of spatio-temporal cumulative distributions.
• R: an environment to perform statistical analysis.
• WinBUGS: a software to perform statistical analysis using MCMC (Gibbs sampling)

Protocols for uncertainty characterisation

• Expert elicitation

Examples

• Qualitative uncertainty analysis: a worked example
• Uncertainty analysis: an example from agriculture
• Uncertainty analysis: an example from waste
• Sensitivity analysis: UVR and skin cancer

References

• Yokota F. and Thompson K.M. 2004a Value of information literature analysis: a review of applications in health risk management. Medical Decision Making 24 (3), 287-298.
• Yokota F. and Thompson K.M. (2004b) Value of information analysis in environmental health risk management decisions: past, present, and future. Risk Analysis 24 (3), 635-650.01
• Morgan M.G. and Henrion M. 1992 Uncertainty: a guide to dealing with uncertainty in quantitative risk and policy analyses. Cambridge: Cambridge University Press, 332 pp.
• Cooke, R.M. 1991 Experts in uncertainty: opinion and subjective probability in science. New York: Oxford University Press, 321 pp.

Monte Carlo simulation

• Metropolis, N. and Ulam, S. 1949 The Monte Carlo method. Journal of the American Statistical Association 44, 335-341.
• Sobol, I. M.A 1949 Primer for the Monte Carlo method. Boca Raton, FL: CRC Press.
• Rubinstein, R. Y. and Kroese, D. P. 2007 Simulation and the Monte Carlo method (2nd ed.). New York: John Wiley & Sons.
• MS Excel Tutorial on Monte Carlo Method

Bayesian statistical analysis

• Gelman, A., Carlin, J.B, Stern, H. and Rubin, D.B. 2003 Bayesian data analysis. New York: Chapman and Hall.
• Gilks, W. 1996 Markov Chain Monte Carlo in practice. New York: Chapman & Hall.

Taylor Series Expansion

• MacLeod, M., A.J. Fraser and Mackay, D. 2002 Evaluating and expressing the propagation of uncertainty in chemical fate and bioaccumulation models. Environmental Toxicology and Chemistry 21(4), 700-709.
• Morgan, M.G. and Henrion, M. 1990 Uncertainty: a guide to dealing with uncertainty in quantitative risk and policy analysis. Cambridge: Cambridge University Press.

Qualitative methods

• IPCC 2005 Guidance notes for lead authors on the IPCC fourth assessment report on adressing uncertainty. Intergovernmental Panel on Climate Change.