Land use regression in IEHIAS
- The text on this page is taken from an equivalent page of the IEHIAS-project.
LUR is based on the principle that pollutant concentrations at any location depend on the environmental characteristics of the surrounding area - particularly those that influence or reflect emission intensity and dispersion efficiency. Modelling is done by constructing multiple regression equations describing the relationship between measured concentrations at a sample of monitoring locations, and relevant environmental variables computed, using GIS, for zones of influence around each site. The resulting equation is then used to predict concentrations at unmeasured locations on the basis of these predictor variables. Prediction can be done either for specific point locations (e.g. residential addresses) or for a fine grid; in the latter case, a raster map of the study area can thereby be generated, and intersected with area-level population data to estimate the exposure distribution.
Scope
Purpose
Land use regression (LUR) was originally developed as a means to assess exposures from traffic-related air pollution, and has since then become a widely used methodology in air pollution epidemiology. Previous studies have shown that, for relatively long-term averaging periods (seasons to years), model performance is comparable with that of formal dispersion models. Although examples are so far rare, it can also be applied to model other forms of pollution, including noise, radioactivity and soil pollution. In the context of integrated environmental health impact assessment it thus offers a useful approach for rapid exposure modelling (e.g. as part of screening studies), and as a substitute for dispersion modelling where the relevant input data or dispersion models are not available.
Boundaries
Applied domain: ambient pollutant concentrations
Applications: pollution mapping and exposure assessment
Constraints: for modelling longer term average concentrations (e.g. annual mean)
Software Requirements:
- geographic information system (GIS)
- multivariate statistical package
Method description
Input
LUR requires the following data:
- Monitoring site locations (x,y coordinates) and concentration data. Ideally, the monitoring newtwork should be regular, or random-stratified on the basis of population distribution. Often, however, data are limited by the extent and configuration of the available national, regional or municipal monitoring network. For most applications a minimum of ca. 30-40 sites is required to develop the LUR model.
- GIS data covering the extent of the monitoring sites and target locations. Data should relate to the primary factors and processes affecting pollutant concentrations including:
- emission source distribution and intensity (e.g. road length, traffic flows, area of industrial land);
- dispersion efficiency (e.g. altitude, windspeed, surface roughness).
- To assess exposures, data are also required either on the geocoded location of individuals/households (address locations), or on population density (e.g. by postcode centroid, census area).
All data should all be in the same projected coordinate system (e.g. National grid, LAEA 5210 ETRS89, UTM).
Output
Output from LUR comprises:
- a regression model describing the association between the predictor variables and measured concentrations;
- predicted concentrations at the monitoring sites, and associated measures of goodness of fit (e.g. R2, standard error of the estimate);
- predicted concentrations at other target locations (obtained by applying the regression model) and/or a map of modelled concentrations.
Estimates of exposure (for individuals) can be obtained by applying the model to point locations representing residential addresses or other locations where people spend their time; if appropriate overall exposures can be estimated by time-weighting the estimated concentrations at each location. Exposure distributions (for population groups) can be estimated by intersecting mapped pollutant concentrations with geocoded data on population density.
In addition, so long as the model includes relevant variables and has been built according to strict logical criteria, the regression equation may be applied to give indicative estimates of potential changes in concentrations or exposure under different policy scenarios (e.g. changes in emission intensity or population distribution).
Rationale
The form of a land use regression model can be written as follows:
where:
Ci</sub> is the modelled concentration at location i;
a is a constant (approximating to the regional background concentration);
bjk is the weight attached to variable j for zone k;
Xijk is the value of variable j, computed for zone k around location i;
e is the error term, representing the unexplained variation in concentrations.
Note that the zones (k) can be unique for each variable (j) - thus different variables can use different buffers or neighbourhoods. Estimates of the constants (a, b, e) are derived using least squares multiple regression analysis at a sample of locations for which measured concentrations are available.
In the original applications of the methodology, models were deliberately constructed to simulate (in a highly simplified way) the physical factors and processes determining air pollutant concentrations. For this reason strict rules were applied in building the models:
- Predictor variables were sought which explicitly represented either source activity (e.g. traffic density, area of industrial land) or dispersion conditions (e.g. altitude).
- Each variable was computed for zones of influence centred on each of the monitoring sites; the shape and size of these zones was selected to reflect the spatial scale of the processes involved;
- Variables were only allowed to enter the equations if they conformed to the predefined direction of effect;
- Variables for any single indicator were allowed to enter the equation only if the zones of influence to which they related provided were contiguous and non-overlapping - e.g. variables for traffic flow for zones of 0-100 and 100-300 metres radius could be included, but not for 0-100 and 200-300 metres (non-contiguous) or for 0-100 and 0-300 metres (overlapping);
- Variables had to be statistically significant at a predefined significance level (5%) .
Several variations on these rules have since been applied. For example, an inclusion criterion of a 1% (absolute) change in R2 has sometimes been used instead of a threshold for significance, and concentrations are often log transformed, both to normalise the data and to guard against prediction of negative concentrations. Some later applications have also tended to relax some of the requirements for model logicality (1 to 3, above). While this has sometimes improved model performance (in terms of R2) in the specific area being studied, it has been at the cost of generating models which are less firmly founded on the physical realities of the pollution system, and consequently which are likely to be less transferable to different contexts or data sets. A rigorous process-based approach to modelling is therefore still to be preferred.
Method
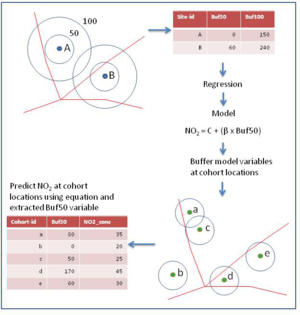
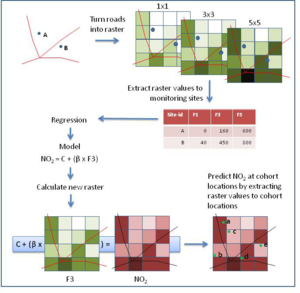
In principle, LUR models could be constructed and used without recourse to GIS. To do so, however, would greatly complicate data extraction and processing. GIS provide a very efficient means both of computing the predictor variables and of mapping the results.
Modelling may be done in a GIS using either vector data (points, lines and polygons) or raster data (uniform grids), as illustrated below. With vector data, the areas are defined using buffering (Figure 1); for LUR models based on raster data, focal functions are used to define and sum the predictor data for a neighbourhood of grid cells (Figure 2).
One of the great advantages of LUR compared to dispersion modelling is that it is computationally relatively simple and efficient. The computational burden increases substantially, however, when vector, rather than raster, data are used. For this reason, raster-based analysis is often preferable when the number of points for which predictions have to be made is large (or when a complete pollution map is required), and/or when data for a large number of variables have to be extracted. Because of the generalisation involved in converting the input data to grids, however, raster-based modelling may be somewhat less accurate.
Details of modelling procedures are thus as follows:
- Collect and pre-process data for a selection of monitoring sites. Ensure that monitoring sites and predictor data sets are in the same projected coordinate system.
- For raster LUR, convert the GIS predictor data sets into rasters with a common specification (e.g. uniform cell size and extent).
- Define the list of predictor variables, including zones of influence (buffer/neighbourhood size) and direction of effect.
- Specify the zones of influence to reflect the scale of environmental processes appropriate for each variable. For example, effects of emissions from road traffic are typically highly localised, so the zones of influence should be narrow - e.g. within a radius of 20m to 500m. Effects of land use are often more extensive and more complex, for land use characteristics affect dispersion patterns as well as emissions; larger zones of influence (up to several km) might therefore be specified. Note that for any variable the minimum buffer size also depends on the resolution of that GIS data set.
- Prior to creating the regression model, carefully review the explanatory variables and note their anticipated direction of effect on pollutant concentrations. Variables that represent emision sources (e.g traffic density) should be positively associated with pollution; variables representing distance from, or absence of, emission sources (e.g. areas of semi-natural vegetation) or the effectiveness of dispersion/mixing processes (e.g. altitude, windspeed) can be expected to have negative associations.
- Use GIS to extract predictor variables for the zones of influence around each monitoring site.
- For vector LUR, use buffer and intersect commands. Note: depending on your GIS software you may have the option to create discrete or dissolved buffers. Do not dissolve!
- For raster LUR, use focal functions to sum each predictor variable for the appropriate neighbourhood of cells (e.g. ArcINFO: focalsum with circle option, ArcGIS: focal statistics with sum and circle option). This will create a new raster for each predictor variable you listed in step 2. Next, as for vector data, extract the values from each raster to the monitoring sites (e.g. ArcGIS: Extract Value to Points).
- Export the monitoring data and extracted predictor variables from GIS and import into the statistical package.
- Develop the LUR model using linear regression. In general apply logical criteria to ensure that the resulting model is interpretable and robust. This is done, firstly, by choosing appropriate explanatory variables and zones of influence to reflect the processes involved. It requires, secondly, the rigorous application of constraints on the regression model (i.e. variable entry and retention needs to be closely supervised). The following guidelines are recommended:
- Try to enter explanatory variables in a ‘supervised-stepwise manner’, so that you include your most important predictors first.
- The sign for each coefficient in the model must conform to the expected direction of effect.
- Each variable in the model should be significant (e.g. p < 0.05) and/or should increase the R2 for the model by a predefined amount (e.g. 1%).
- Variables entered later in the process should not be retained if they cause variables already in the model to become invalid according to guidelines 2 or 3.
- Avoid double counting by excluding overlapping buffers. For example, including roads in 0-20m and 20-40m is valid, but including roads in 0-20m and 0-40m is not.
- Gaps in the buffers should also be avoided. For example, roads in the 20-40m buffer should not be included unless roads in the 0-20m buffer are already in your model.
- The LUR model should be validated, and performance statistics reported, either by using a reserved set of monitoring data or through cross-validation techniques (e.g. leave-one-out analysis).
- Apply the LUR model.
- For vector LUR, first compute relevant buffered variables for the target locations (e.g residential addresses); then apply the regression equation. If a full pollution map is required use an appropriate method of spatial interpolation (e.g. kriging).
- For raster LUR, apply the regression to the relevant rasters generated in step 3 to derive a final exposure raster (e.g. ArcINFO local grid operators to perform a cell-by-cell calculation; ArcGIS: Raster Calculator).
- Inspect the map to ensure that the mapped dustribution is sensible. If it is not, reconsider:
- the choice of monitoring sites used to develop the model (e.g. identify and exclude outliers; fillin gaps in the geographic coverage or in specific subzones);
- the range of predictor variables offered into the model;
- the choice of buffer zones;
- the rules for model-development;
- the spatial resolution and scale.
References
- Hoek, G., Beelen, R., Pebesma, E., Vienneau, D., de Hoogh, K. and Briggs D.J. 2008 Mapping of air pollution at a fine spatial scale across the European Union. Science of the Total Environment 407, 1852-1867.
- Vienneau, D., de Hoogh, K., Beelen, R., Fischer, P., Hoek, G. and Briggs, D.J. 2010 Comparison of land-use regression models between Great Britain and the Netherlands. Atmospheric Environment 44, 688-696.
