Transport and transformation in environmental media
- The text on this page is taken from an equivalent page of the IEHIAS-project.
Once released into the environment, pollutants are subject to a range of transport and transformation processes. They are dispersed both through bulk transport (i.e. carried along by the surrounding medium) and by diffusion (movement of individual molecules or particles, down the concentration gradient - i.e. from higher to lower concentration zones). En route, they are diluted by mixing within the transport medium and transformed by both chemical reactions and physical processes such as abrasion, and selectively removed by gravitational settling, scavenging and filtration. As a result, concentrations tend to decline with both distance and duration of transport, and new (transformed) pollutants tend to develop, which may themselves be potentially harmful for humans. In order to estimate exposures and risks for human health, therefore, we need to understand and quantify the effects of these transport and transformation processes.
Factors determining patterns and rates of transport and transformation
The strength of the processes involved, and thus the consequences in terms of pollution concentrations, depends on the nature of the environmental medium and of the pollutants concerned. Typically, bulk transport processes dominate, so how far and how quickly pollutants spread is governed by the rate of movement of the medium in which they occur - by windspeed, water velocity etc. Many chemical processes are also temperature (and often moisture) dependent, so rates of transformation are affected by climate and weather. The local micro-environment also has a powerful influence, for example by determing opportunities for filtration and sedimentation.
Measuring and modelling the effects of transport and transformation
Information on the fate of the pollutants as they pass through the environment can clearly be obtained to some extent from direct measurement - e.g. by monitoring pollutant concentrations at a sample of locations. A large number of databases exist providing such data, often based on routine monitoring for purposes of policy compliance, and links to a number of sources (and detailed factsheets on a selection) are provided in the Data section of the Toolkit. As with other aspects of assessment, however, the value of direct measurements are limited, both by the cost and logistical difficulties of monitoring (which mean that data are often sparse and not necessarily representative) and because many assessments require information relating to scenarios which have not yet taken place. To a large extent, therefore, assessments rely on modelling of transport and transformation processes.
The models that have been developed vary between different envitonmental media, not only because the processes of transport and transformation differ, but also because the scientific disciplines involved are often somewhat independent and the extent to which modelling has evolved varies. Generally, modelling is better developed for air pollution than for other media. Further information on the approaches taken in these different fields, and on the specific modelling techniques used, is given via the links in the panel to the left (see also link to ExpoPlatform, below).
In recent years, however, efforts to devise more integrated multi-pollutant and multi-media models have also been made. In addition, many environmental transport and transformation processes can be simulated by relatively simple spatial functions, so a range of more generic modelling methods have been developed using GIS. Further information on these various modelling approaches, and access to specific methods and tools, is also given via the links to the left.
Air pollution
Although most people spend most of their time indoors, policies on air pollution (and most epidemiological studies of air pollution) have tended to focus on the ambient (or outdoor) atmosphere. In the case of health impact assessments, there is some danger in this focus, for it can ignore many of the behavioural and micro-environmental factors that influence exposure, and which can be manipulated to protect health. While many assessments therefore need to model patterns and processes of outdoor air pollution, this may not be the end of the story, and information may also be required on indoor air.
Modelling ambient concentrations
Reflecting the needs of policy, the majority of the air pollution models that have been developed to date are targetted at estimating ambient concentrations. While a wide variety of models has been developed, two general approaches can be recognised:
- dispersion models, which attempt to simulate the physical (and to some extent chemical) processes involved in transport;
- statistical models, which largely ignore the intervening processes, but represent the relationship between the source and concentrations at the receptor in the form of (empirically-informed) formulae or statistical functions.
The distinctions between these two approaches is not always clear, and various hybrid techniques have been developed. In most cases, however, dispersion models are to be favoured for the purpose of impact assessment, because they more explicitly represent the real-world processes that occur, and should therefore be more reliable as a basis for prediction (see link in panel to left). Their use is nevertheless limited in some cases by constraints of data or the heavy processing requirements and software costs. In these circumstances alternative approaches may be more appropriate. Moreover, ambient air pollution models only provide reliable estimates of actual exposure where:
- exposures from indoor sources are not of interest (e.g. policies focused on outdoor concentrations and ambient exposures)
- outdoor to indoor penetration of the pollutant of interest is relatively high and consistent (e.g. PM2.5)
- the target population can be assumed to remain stationary in relation to the concentration field (e.g. secondary air contaminants).
Where these conditions do not apply, results need to be linked to indoor air pollution models that can represent the transfers and transformations that take place as pollutants pass into buildings, and/or the additional influence of indoor sources.
Modelling indoor concentrations
As with ambient pollution, methods for modelling indoor concentrations vary. Where the focus is on pollutants which are largely derived from outdoor sources, the simplest approach has been to assume a constant ratio between outdoor and indoor concentrations. Where indoor sources are of greater concern, categorical models have been developed, using the presence or absence of specific emission sources (e.g. cooking, heating) as an indicator of likely indoor concentrations. More realistic models require that account is taken of the mixing, air exchange and transformation processes that can occur both within the indoor environment, and between indoors and outdoors. To represent these, some form of mass-balance or fluid dynamic model is likely to be necessary.
Atmospheric dispersion models
Two fundamentally different types of atmospheric dispersion model can be identified, both based on physical dispersion equations and description of the ground surface topography: Lagrangian models and Eulerian models.
Lagrangian models
Lagrangian models take different forms. The most widely used are Gaussian models. These are mechanistic models, based on turbulent eddy mixing theory, and predict for each model run a downwind ground-level concentration field of the emitted pollutant, centred on the centreline of the plume. They are primarily designed to predict short term concentration fields downwind from a source (point, line or area), but can be extended to long term average ground level concentration fields and concentration probability distributions. In the latter case, they require extensive meteorological, topographical, source location and emission time which series data. They are particularly suited for elevated point sources (e.g. power plant chimneys),
Eulerian models
Eulerian dispersion models are mechanistic, based on fluid dynamics. They are designed to model high resolution concentration fields, which can be averaged to provide estimates of long term concentrations. They are particularly suited for modelling concewntrations and exposures associated with complex sources, distributed over an area (e.g. road traffic).
Limitations
Uncertainties in dispersion models need to be recognised. These derive both from the inevitable simplification of the complex real-world processes that they entail, and from limitations of the available input data (e.g. on emission sources and meteorology). Models tend to be most reliable in relatively open, uncluttered conditions, and for estimation of longer term (daily, annual) concentrations.
Because they consider only ambient concentrations, dispersion models do not provide direct estimates of human exposure. In many situations, however, ambient concentrations can be used as an indication of potential exposures and, where indoor exposures are of concern, they can be linked to indoor air pollution models.
Statistical air pollution models
Statistical models of air pollution have been developed primarily to provide a simpler and less data-demanding approach to estimating atmospheric concentrations, either for the purpose of air quality management (e.g. as screening models) or for exposure assessment in epidemiological studies. A range of approaches have been devised, so that statistical models take many different forms. Amongst these, two approaches are of particular utility in exposure assessment:
- simplified dispersion models, in which the dynamic transfer equations have been reduced to a series of formulae;
- GIS-based models, where associations between source and receptor are represented by empirically defined equations, derived using regression analysis or similar techniques.
Simplified dispersion models
These typically represent an attempt to reduce the complex, dynamic equations inherent in a true dispersion model to a simpler, and generally static, form. Simplification is achieved primarily by ignoring the local, time-varying processes that affect short-term air pollutant concentrations (e.g. associated with variations in meteorology), and modelling instead the average (net) long-term patterns. Models thus comprise a series of formulae or statistical equations, which can be solved either arithmetically (e.g. using spreadsheet functions) or through the use of look-up tables and graphs.
Amongst many examples, two of the most widely used in Europe are the Calculation of Air pollution from Road traffic (CAR) model and the Design Manual for Roads and Bridges (DMRB) model. The original CAR model was developed for use as a screening tool for air quality management in the Netherlands, but a more generic version (CAR-International) was later devised. The DMRB model was designed to support air quality management in Britain, and likewise has undergone several revisions; the most recent provides the means to run it within a GIS. Both models have been widely tested and compared against other, more sophisticated appraoches, and have generally been shown to work well when used within their intended operating conditions (i.e. to assess locally-derived concentrations of traffic-related air pollutants in relatively simple source-receptor environments). They are, however, inevitably limited in that they are not designed to deal with non-transport emissions, and in terms of the sources number of sources and receptors that can easily be analysed, or their ability to model long-range transfers of pollutants.
GIS-based models
Geographical information systems (GIS) have become important tools for air pollution modelling, due to their capability to extract and process the spatial data needed as inputs to air pollution models, and then to map the results of the models.
In recent years, however, GIS have also been used to develop air pollution models in their own right. One such approach has been termed 'land use regression' (LUR), because it is based on empirically-derived regression equations linking land use (or more strictly land cover) to measured air pollutant concentrations at a set of monitoring sites. Other predictors are usually selected to represent traffic-related emissions (e.g. road length, traffic flows) in the surrounding area, and the effect of local topography (e.g. altitude). Optimal models (in terms of the correlation between measured and predicted concentrations) can often be obtained using stepwise regression techniques, in a somewhat unconstrained way. This, however, carries the danger of developing models which are inherently counter-intuitive, and which may not be generally applicable. Ideally, therefore, LUR models should be developed according to strict rules on variable selection, designed to reflect the real-world processes and dependencies that determine air pollutant concentrations.
An alternative to LUR modelling has recently been devised, using focalsum techniques in GIS. This explicitly uses measures of source intensity or emissions as inputs, and applies inverse-distance functions to weight these according to their contribution to air pollution at the monitoring sites. The weights may be determined a priori (e.g. on the basis of results from dispersion modelling under typical conditions), or by using regression modelling.
In both cases, model development requires a dense network of monitoring sites, so has usually been done using purpose-designed monitoring campaigns (e.g. employing passive samplers). In both cases, also, model performance has been shown to be good (and comparable to dispersion models) when used to analyse relatively long-term (e.g. seasonal, annual) concentrations of locally-derived pollutants. These methods also have an advantage of relative ease of application, and less demanding processing requirements, than dispersion models. On the other hand, a major limitation is that the models do not directly represent the processes determining air pollution concentrations, so cannot be guaranteed to provide reliable estimates of changes in concentration associated with policy or other interventions. Their use in integrated assessments, therefore, is mainly as screening tools.
Indoor air pollution models
Background
Indoor air pollution models provide estimates of indoor concentrations of contaminants derived from external and/or internal sources. Models have mainly been developed for the purpose of building design, but have variously been adopted and adapted for use in epidemiological and health impact studies.
A range of models have been applied in this context. The most widely used are dilution (or ventilation) models. These simulate changes in concentrations of contaminants under the influence of atmospheric mixing within a room, and air exchange with the outdoor environment and/or between rooms.
Two main approaches to dilution modelling may be identified: mass balance models and computational fluid dynamic (CFD) models. The simplest (mass balance) models apply for a single compartment (i.e. a room where the source, ventilation and the exposed target occur), steady state conditions and complete mixing. Multi-zone models are also available to simulate more complex situations, with several interconnected compartments. The most advanced (CFD) models deal with dynamic conditions, including changing or intermittent release and ventilation, multiple interconnected compartments and displacement ventilation. Indoor air chemistry, sedimentation and absorption (deposition) of pollutants indoors can also be incorporated into the models.
Principles
Dilution models are mechanistic in that they are based on simplified physical mixing, yet often semi-empirical - i.e. adjusted by empirical correction factors for different air ingress and egress configurations and room characteristics. The models are deterministic: with appropriate input data, the same model applies for any indoor space – usually the home or workplace of an individual. If, however, full ranges and distributions of the input data are available (e.g. for the rooms in a large office building, or homes in a suburb), dilution models can be run for probabilistic simulation of the whole range of indoor exposure concentrations for the target population.
For general modeling of exposure to contaminants released into the indoor air, dilution models often lack important terms: decay, e.g. absorption to room surfaces and furnishings; removal, e.g. filtration by air cleaning devices; medium transfer, e.g. sedimentation and absorption from air to dust; and contact rate/time.
In the simplest formulations, with assumptions of steady state conditions and complete mixing, the indoor concentration (C) is seen as the product of a constant source term (m) (mass/time) and ventilation rate (Q) (volume/time)
C = m/Q
Incomplete mixing is dealt with by a dimensionless empirical correction factor (0 < c < 1.0), in which c = 1.0 would indicate complete mixing:
C = m/c۰Q
Displacement ventilation is often used in large rooms. This avoids mixing fresh and used indoor air, and instead gently flows fresh cool air below the used and warmed up room air, pushing it upwards to exhaust vents. In dilution modeling this is treated simply by giving the empirical correction factor a value higher than 1.0 (c ≥ 1.0).
A source release starting at time t = 0 leads to an indoor concentration (in room of volume V) that asymptotically changes towards the steady state.
C(t) = m۰e^-(V/Q۰t)^/c۰Q
Stopping the source release at any point of time leads to a similar concentration decay towards zero. Instantaneous releases are incompatible with complex mixing: in reality, mixing is not instantaneous. Indoor concentrations from instantaneous releases can therefore be modeled only from the time required for complete mixing (t~cm~). If the source release and/or ventilation rate can be expressed as mathematical function(s) of time, the most complicated single compartment model thus becomes:
C(t) = m(t)۰e^-(V/Q(t)۰t)^/c۰Q(t)
The contribution of pollution from outdoor air to indoor exposure can be incorporated simply by adding the outdoor air concentration, corrected if necessary by an indoor/outdoor removal term.
More complicated cases of dynamic releases and ventilation, multiple interconnected compartments, incorporation of decay and removal by indoor air chemistry or pollutant deposition on indoor surfaces require increasingly complicated and often numerical dilution models.
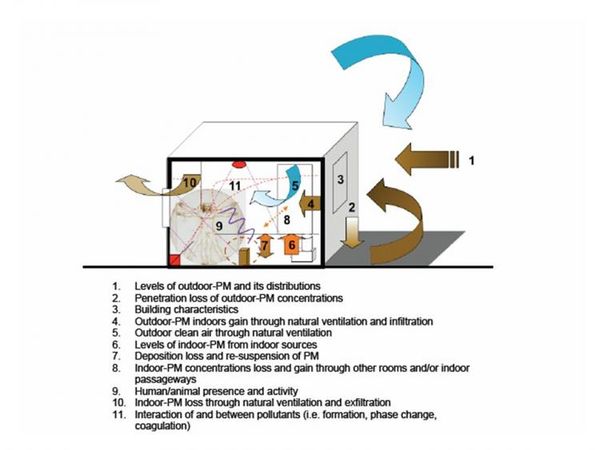
The figure below summarises the main factors and processes affecting indoor concentrations of particulates.
Recommended models for indoor air pollution are given in ventilation handbooks and the legally binding ventilation codes. The National Institutes for Standards and Technology (NIST), the American Society of Heating, Refrigerating, and Air-Conditioning Engineers (ASHRAE) and the Air Infiltration and Ventilation Centre (AIVC) are examples of organisations with ventilation modelling resources.
Water quality
In terms of human health, the main concerns about water pollution relate to contamination in drinking water. In Europe, where the vast majority of households are served by piped water, this puts the focus on public water supplies. It is nevertheless important ro remember that exposures to contaminants do not only occur by drinking treated water; showering and bathing, swimming (in both treated pools and in lakes, rivers or the sea), and water handling (e.g. for irrigation) can all be responsible for significant exposures. In addition, water supply to the tap is merely the last link in a long chain, which draws water from a range of natural sources, including surface and groundwaters. Opportunities for contamination occur throughout this chain.
Approaches to modelling
Models of water quality are therefore concerned with trying to estimate and simulate the processes involved from initial source (e.g. as rainfall) to ultimate exposure. Three main elements of this chain are of particular importance, and because the processes involved in each case are somewhat different each tends to be associated with different types of model:
- Surface runoff
- Groundwaters
- Treatment and public supply
In each case, different approaches to modelling may be used.
Statistical models, derived from the analysis of measured data in a sample of locations, are often applied to give relatively simple predictions of variations in water quality either through time or over space. These use empirically observed relationships between measured pollutant concentrations at sample locations (or times) and characteristics of the surrounding environment (e.g. land cover/use, soils, stream discharge, meteorology) as a basis for predicting variations in pollutant concentrations either through time or over space. Where the focus is on predicting spatial patterns, models are often constructed in GIS, in order to facilitate data linkage, analysis and mapping.
Process models have widely been developed for engineering purposes (i.e. to help manage water supplies). These attempt to simulate the processes operating within the hydrological system, and often comprise a number of linked sub-models, representing the different compartments of the system - e.g. the soil, surface runoff and stream in the case of surface water. They also tend to involve two different types of model: hydrological models which describe the processes by which precipitation passes into and through the water body (e.g. the stream or aquifer); and solute models which describe the processes by which contaminants are released into or picked up by the water, en route. A large number of models serving part or all of these processes have been developed.
In general, statistical models have the advantage of simplicity and ease of application, but may be less reliable as a basis for prediction beyond the realm of the measured data on which they are based. Process models are more robust in this respect, but they are relatively complex and have somewhat daunting data demands: lack of the relevant input data, or uncertainties in the data that do exist, may therefore be significant limitations. Care is also needed, because most models have been developed to represent specific environmental conditions (e.g. climate, topography, land use, geology or soil types), and may not be applicable in other contexts. In an attempt to exploit the differing advantages of both approaches, hybrid models, comprising both statistical and process-based elements, are also often used.
Non-ionising radiation
Non-ionising radiation is electromagnetic radiation that lacks the energy entirely to remove electrons from an atom or molecule. It covers a range of wavelengths, from a narrow section of the ultraviolet (UV) and visible spectrum through infrared, microwave and radio frequencies (RF), into extremely low frequency (ELF) bands. Exposure sources also vary across this spectrum. While the majority of UV and visible radiation comes from natural sunlight, the lower frequency bands derive mainly from artificial sources, including electrical equipment, telecommunications infrastructure/appliances and powerlines.
Ultraviolet radiation
In the case of ultra-violet radiation from the sun, known health effects from exposures to UV radiation include skin cancers and corneal damage (burns and cataracts). Over recent decades, the incidence of these effects appears to be growing, due in part to changes in behaviour (and perhaps climate change) which have increased exposures.
Exposures to UV radiation are generally modelled using radiative transfer models (or simplifications of them), that attempt to simulate the processes involved in transmission and scattering of solar radiation as it passes through the atmosphere and interacts with the ground surface.
Links to models and to an example of how they can be applied to estimate exposures to UVR are provided under See also, below.
Electromagnetic radiation from telecommunications systems
Definitive evidence for health effects of ectro-magnetic radiation from artificial sources, at levels commonly encountered in the open environment, is lacking, and plausible mechanisms have not been firmly identified. Nevertheless, public concern remains high, not least about possible risks (e.g. brain cancer) from powerlines, mobile phones and associated base stations. Precautionary measures to limit public and occupational exposures from these sources have therefore been introduced.
Exposures to non-ionising radiation from artificial sources are modelled using a range of approaches, including empirically-calibrated path loss models, ray-tracing models, and statistical models. Many of these have been developed and tested only for specific wavelengths and in a limited range of circumstances, so their extrapolation to other contexts needs to be done with care.
See also
UV Radiation:
EMF Radiation:
GIS-based models
Geographical information systems (GIS) offer powerful technologies for use in integrated assessments. Their power comes from the fact that they provide a means:
- to link and integrate different data sets from different sources - e.g. between different environmental phenena or between environment and population;
- to explore and analyse spatial patterns and relationships in the data - e.g. to estimate numbers of people potentially exposed because they live close to emission sources;
- for spatial modelling - e.g. to simulate propagation and dispersion of environmental pollutants;
- for mapping and other forms of visualisation of spatial data.
Spatial data types
While, in practice, almost all real-world phenomena comprise volumes (i.e. they have dimensions of height, width and depth), the data that we use to describe them often represent them in different ways. Three fundamental spatial structures can be recognised:
- points - e.g. a sampling location, a point emission source, or a residential address;
- lines - e.g. the centreline of a roadway or stream;
- areas - e.g. an area of woodland or industrial land, a census tract, a country.
Each of these, however, can be represented either as an irregular structure or as a regular one. Most natural phenomena are somewhat irregular: for example, sampling locations are spread unevenly across the landscape, roads are laid out haphazardly, and administrative regions are bounded by irregular boundaries. In GIS, these irregular structures are all represented by vector data.
In many cases, however, it is advantageous to present data in a regular form - as an array of points, a lattice of lines, or a grid of regular cells. In GIS, these are all forms of raster data. Although presenting data in this form may involve some degree of distortion of reality, it has several major advantages. In particular, it makes computation much more efficient (and therefore allows larger data sets to be analysed) and, as a basis for mapping, improves interpretability of the results. For these reasons, many of the most powerful GIS techniques operate in raster form, and in many cases it is helpful to present results as gridded maps.
GIS-based modelling techniques
Because of their great flexibility (and the large range of different modelling tools that they contain) GIS offer a huge range of different modelling techniques. As implied above, many of these are restricted to (and designed to be used with) specific data types. The table below outlines five general approaches that have special utility for exposure modelling in integrated impact assessments. Further information is provided on a number of these via the embedded links and the panel to the left.
| Technique | Data types | Description | Examples of applications |
|---|---|---|---|
| Interpolation | Points | Estimates conditions at unsampled (intermediate) locations by fitting a surface through the data points. Range of methods including Kriging, splines and inverse distance weighting. Mainly applied to point data, but can also be used with areas. | To model air pollution surfaces based on data from an air pollution monitoring network |
| Buffering | Points | Creates buffer zones of specified radius around a set of target locations, in order to explore relationships with their surrounding areas. Target locations are often points, but buffering can also be applied to lines and areas. Searches within the buffer zones can be made for point, line or area features. Multiple buffer zones can be generated and analysed. |
|
| Focal sum | Raster | Calulates the weighted sum of values in surrounding grid cells for a series of focal (target) cells. Kernel files of different shape (e.g. rectangular, circular, elliptical) can be applied to represent the weights for surrounding cells. Weights can be derived from a specified model (e.g. based on distance from the focal cell) or applied uniquely to each cell in the kernel file. Though commonly applied using summation (focal sum), other statistical measures (e.g. average, range) can also be used. | To model air pollution as the distance-weighted sum of emission or source intensity in surrounding areas. |
| Network analysis | Lines | Models accessibility along a line network by computing the total cost or impedance between two points. Cost can be based on connective distance (i.e. distance along the network) or on other (attached) attributes of the network (e.g. travel time). |
|
| Hydrological models | Raster | Models flow routes through a gridded area (raster) from a start point (seed) to exit point. Preferred routes between adjacent cells are defined on the basis of a simple optimising rule (e.g. maximum downward gradient). Mainly used for modelling hydrological processes, but can also be more generally applied to any diffusion process. | To model surface runoff of rainfall in a catchment. |