Human PBPK model for dioxin: Difference between revisions
(→Assumptions: first version of Bayesian hierarchical model of sarcoma data) |
|||
| Line 414: | Line 414: | ||
library(ggplot2) | library(ggplot2) | ||
datall <- read.csv("V:/TUSO/Projects/POPit ja lihavuus/Sarkoomakyselydata/Copy of sarkooma_kysely_ja_dioksiinit_korjattu.csv", header = TRUE, skip = 0) | datall <- read.csv("V:/TUSO/Projects/POPit ja lihavuus/Sarkoomakyselydata/Copy of sarkooma_kysely_ja_dioksiinit_korjattu.csv", header = TRUE, skip = 0) | ||
congeners <- colnames(datall)[330:388] | |||
dat <- datall[c(1:3, 10:13, 78, 168:176, 199:201, 330:388)] | dat <- datall[c(1:3, 10:13, 78, 168:176, 199:201, 330:388)] | ||
dat <- melt(dat, measure.vars = 21:79, variable.name = "Congener", value.name = "Result") | dat <- melt(dat, measure.vars = 21:79, variable.name = "Congener", value.name = "Result") | ||
| Line 420: | Line 421: | ||
dat$V <- dat$Paino * dat$rasvaprosentti | dat$V <- dat$Paino * dat$rasvaprosentti | ||
dat$D <- dat$Maitolihakala * 10 | dat$D <- dat$Maitolihakala * 10 | ||
Y <- length(congeners) #number of congeners and j's in for loop | Y <- length(congeners) #number of congeners and j's in for loop | ||
| Line 433: | Line 433: | ||
mo <- textConnection("model{ | mo <- textConnection("model{ | ||
r ~ dunif(-0.06, 0) | |||
tau_C ~ dunif(0.001, 1000) | |||
for (j in 1 : 3 ) { # for testing reduced to 3 congeners, real loop amount is Y | |||
k[j] ~ dunif(0.1, 50) | |||
} | |||
for( i in 1 : N ) { | |||
C[i] ~ dnorm(mu_C[i], tau_C) | |||
mu_C[i] <- log(Dn[i]) * (exp(a[i] - r - k[Congener[i]])*t[i] - 1)/(V[i]*(a[i]-r-k[Congener[i]])) | |||
} | |||
} | } | ||
") | ") | ||
dataList = list( | dataList = list( | ||
| Line 449: | Line 449: | ||
Congener = as.numeric(compdat$Congener), | Congener = as.numeric(compdat$Congener), | ||
N = nrow(compdat), | N = nrow(compdat), | ||
# n = length(unique(dat$kysely_id)), #number of patients in study | # n = length(unique(dat$kysely_id)), #number of patients in study | ||
t = compdat$t, | t = compdat$t, | ||
a = compdat$a, | a = compdat$a, | ||
| Line 467: | Line 467: | ||
Meanorig = aggregate(compdat$Result, compdat["Congener"], mean), #calculate mean for original data | Meanorig = aggregate(compdat$Result, compdat["Congener"], mean), #calculate mean for original data | ||
Sdorig = aggregate(compdat$Result, compdat["Congener"], sd)$x, #calcaulte sd of original data | Sdorig = aggregate(compdat$Result, compdat["Congener"], sd)$x, #calcaulte sd of original data | ||
# Meanlog = aggregate(Compound, compdat["Congener"], mean)$x, #calculate mean for logdata | # Meanlog = aggregate(Compound, compdat["Congener"], mean)$x, #calculate mean for logdata | ||
# Sdlog = aggregate(Compound, compdat["Congener"], sd)$x, #calculate sd for logdata | # Sdlog = aggregate(Compound, compdat["Congener"], sd)$x, #calculate sd for logdata | ||
Meanpost = c(mean(out[[4]][[1]]), #calculate mean of mu for posterior (test 4) | Meanpost = c(mean(out[[4]][[1]]), #calculate mean of mu for posterior (test 4) | ||
mean(out[[4]][[2]]), | mean(out[[4]][[2]]), | ||
| Line 481: | Line 481: | ||
oprint(resultsall) | oprint(resultsall) | ||
ggplot( | ggplot(compdat, aes(x = Result, colour = Congener))+geom_density()+scale_x_log10() | ||
</rcode> | </rcode> | ||
Revision as of 09:45, 5 April 2016
| Moderator:Jouni (see all) |
|
|
| Upload data
|
Question
How to calculate dioxin concentrations in human tissues after a given exposure pattern?
Answer
These are several approaches available.
Tuomisto et al model
- This model was previously on page Dioxin.
| Obs | Congener | Market basket | TEF | Elimination constant | Half life |
|---|---|---|---|---|---|
| 1 | TCDD | 2 | 1 | 0.00026 | 7.3 |
| 2 | 12378PeCDD | 2 | 1 | 0.00017 | 11.2 |
| 3 | 123678HxCDD | 5 | 0.1 | 0.000145 | 13.1 |
| 4 | 1234678HpCDD | 7 | 0.001 | 0.00039 | 4.9 |
| 5 | OCDD | 60 | 0.0003 | 0.00028 | 6.8 |
| 6 | TCDF | 8 | 0.1 | 0.0009 | 2.1 |
| 7 | 23478PeCDF | 16 | 0.3 | 0.00027 | 7.0 |
Dioxin kinetics with Bayes


- This code works only if you first get the data.frame dat. It was originally produced with the code KTL Sarcoma study#Data management. Data files from the study must be available to produce dat.
| WHOTEQ | mu | |
|---|---|---|
| Pearson | ||
| Observed WHOTEQ | 1.000000 | 0.380774 |
| Predicted mu | 0.380774 | 1.000000 |
| Spearman | ||
| WHOTEQ | 1.0000000 | 0.5486548 |
| mu | 0.5486548 | 1.0000000 |
Aylward et al model
TOXI/INERIS model
| Dioxin PBPK model |
|---|
| The results are total amounts (ng) of dioxin, except blood concentration (ng/l). |
The input data used for this variable:
|
Rationale
Tuomisto et al

The generic one-compartment model says that at a steady state, input and output mass rates of the compound are equal:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = C k V,}
where C is concentration and thus equals m / V, k is elimination constant, V is distribution volume, and m is the mass of compound in the body.
This model is based on one-compartment kinetics with a dioxin intake trend (assuming a constant relative change r in time). i is a timepoint in history and ti means the distance in time between timepoint i and now (n). The concentration of dioxin in the body now because of a dose Di at timepoint i (cn,i) is calculated as follows, assuming that k is the elimination constant for dioxin, Dn is dose now, and the dose during time changes at a constant rate r (we assume that dose D was repeating at every timepoint between i and now, just gradually changing in intensity). We also assume that the distribution volume (in practice, amount of fat in the body) changes with rate a. All changes (elimination, intake, and distribution volume) are relative and thus follow exponential function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{n,i} = \frac{D_i}{V_i} e^{-k t_i} = \frac{D_n e^{-r t_i}}{V_n e^{-a t_i}} e^{-k t_i} = \frac{D_n}{V_n} e^{(a-r-k) t_i}.}
The total dioxin concentration now Cn,i from all doses during the time period between i and now is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n,i} = \int_0^{t_i} \frac{D_n}{V_n} e^{(a-r-k) t}dt = \frac{D_n}{V_n} (\frac{e^{(a-r-k) t_i}}{a-r-k} - \frac{e^{(a-r-k) 0}}{a-r-k}) = \frac{D_n (e^{(a-r-k) t_i}-1)}{V_n(a-r-k)}.}
Current intake can be solved from here, given current dioxin concentration:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_n = \frac{C_{n,i} V_n(a-r-k)}{e^{(a-r-k) t_i}-1}.}
Current dioxin concentration can also be given in terms of intake at time i rather than intake now as Dn = Di er ti:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n,i} = \frac{D_n (e^{(a-r-k) t_i}-1)}{V_n(a-r-k)} = \frac{D_i e^{r t_i} (e^{(a-r-k) t_i}-1)}{V_n(a-r-k)} = \frac{D_i (e^{(a-k) t_i}- e^{r t_i})}{V_n(a-r-k)}.}
The elimination of dioxins occur almost exclusively in the liver, and therefore liver concentration is the physiological determinant of this first-order kinetic elimination. Dioxin liver concentration correlates very well with fasted blood concentration and fat tissue concentration but NOT with body burden (if fat weight varies). So, if the amount of body fat changes during the follow-up period, it must be adjusted.
If we think about fat weight change as a process where the distribution volume increases in such a way that (otherwise unchanged) concentration decreases exponentially, then we can describe this dilution as if it was another decay process with decay rate a.
If we know the fat weight at time i and now, we can estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_n = V_i e^{a t}}
where Vi and Vn are distribution volumes at i and now, respectively. By solving we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln\frac{V_n}{V_i} = at \Leftrightarrow a = \frac{ln \frac{V_n}{V_i}}{t}.}
For a previous attempt to calculate this using exponential integral function, see[2].
More complex situations
There may also be a single additional dioxin bolus at timepoint A, and this is denoted dA:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{n,i} = \frac{D_n}{r-k} (e^{(r-k) t_i}-1) + b_A e^{-k t_A}.}
Also, there may be a breast feeding period during the observed time span
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{n,i} = (\frac{D_n}{r-k} (e^{(r-k) t_i}-1) + b_A e^{-k t_A}) (1 - (1-e^{-k_B t_B})(e^{-k t_S})),}
where kB is the elimination constant caused by breast feeding, tB is the duration of breast feeding, and tS is the time since the breast feeding. ⇤--#: . There is an error in the equation with breast feeding? --Jouni (talk) 11:43, 22 March 2016 (UTC) (type: truth; paradigms: science: attack)
From this, we can solve Dn:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_n = \frac{(r-k) (M_{n,i} - b_A e^{-k t_A} (1 - (1-e^{-k_B t_B})(e^{-k t_S})))}{(e^{(r-k) t_i}-1) (1 - (1-e^{-k_B t_B})(e^{-k t_S}))},}
which can then be used as an independent variable in food intake regression models. This simplifies to
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_n = \frac{(r-k) M_{n,i}}{(e^{(r-k) t_i}-1) (1 - (1-e^{-k_B t_B})(e^{-k t_S}))},}
if there is no bolus, and even further
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_n = \frac{(r-k) M_i}{e^{(r-k) t_i}-1},}
if there is no breast feeding.
If the intake is constant and there is no breast feeding, the previous equation solving Mi simplifies into
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{n,i} = \frac{D_n}{k} (1 - e^{-k t_i}) + b_A e^{-k t_A},}
where Dn/k is the steady state amount of dioxin in the body at constant intake, (1 - e-k ti) is the relative deviation from the steady state, and bA e-k tA is the burden from the additional dioxin bolus at A.
Bayesian hierarchical model
Assumptions
- WHO-TEQ intake 57 pg/d average (Kiviranta et al, Env Int 2004:30:923)
- low intake 40 pg/d (42,05)
- high intake 160 pg/d (168,2)
- Average distribution 56 pg/d animal products, 1 pg/d plant products (ibid)
- low intake 39 pg/d animal products, 1 pg/d plant products
- high intake 157 pg/d animal products, 3 pg/d plant products
- Congener distribution as pg TEQ (rounded)
- low intake TCDD 7,9, 12378PCDD 7,9, 123678HxCDD 2, 1234678HpCDD 0,03, OCDD 0,07, TCDF 3,2, 23478PeCDF 19 pg/d WHO-TEQ
- high intake TCDD 32, 12378PCDD 32, 123678HxCDD 8, 1234678HpCDD 0,1, OCDD 0,3, TCDF 12,6, 23478PeCDF 76 pg/d WHO-TEQ
- Congener distribution as pg (rounded, rounded numbers used in other sheets)
- low intake TCDD 7,9, 12378PCDD 7,9, 123678HxCDD 20, 1234678HpCDD 28, OCDD 237, TCDF 32, 23478PeCDF 63 pg/d
- high intake TCDD 32, 12378PCDD 32, 123678HxCDD 80, 1234678HpCDD 111, OCDD 948, TCDF 126, 23478PeCDF 253 pg/d
- Congener elimination constants (d-1) TCDD 0,00026, 12378PCDD 0,00017, 123678HxCDD 0,000145, 1234678HpCDD 0,00039, OCDD 0,00028, TCDF 0,0009, 23478PeCDF 0,00027
- Half lives from Milbrath et al., Environ. Health Persp. 2009:117:417-425
TOXI/INERIS
- This model description has been taken from an equivalent page of the IEHIAS-project. For the main article about dioxins, see Dioxin.
Basic info
| Last modification: | 04/07/2007 | Model version : | |
| Software status : | Free software | OS : | Linux |
| Supplier : | INERIS | Installation : | See source |
| Possible developments : | yes | Source : | TOXI/INERIS web site [3] |
| Supplier address: | INERIS Verneuil en Halatte, France | Referent(s)* : | S. MICALLEF (INERIS)
Sandrine.micallef@ineris.fr |
Discipline : keywords: toxicokinetic model, 2,3,7,8-tétra-chloro-p-dioxin (TCDD), PBPK
Scope of the mode
Physiologically Based Toxicokinetic (PBTK) model for Dioxine. The presented PBTK model allows to simulate ingestion exposures to 2,3,7,8-tétra-chloro-p-dioxin (TCDD) for a woman over her whole life. TCDD is a persistent chemical found in trace amounts all over the globe. It accumulates in animal fat all along the trophic chain. Human exposure to TCDD is therefore almost unavoidable, even if in trace amounts. TCDD has multiple effects on health.
Model description
The proposed model is based on a previous one proposed by van der Molen and colleagues in 1996[4]. The model computes various measures of internal dose as a function of time. The superposition of a peak exposure to a time-varying background intake can be described. All ingested TCDD is supposed to be absorbed. TCDD is supposed to distribute between blood, fat, muscles and skin, and viscera. The model equations are solved dynamically (by numerical integration) with the MCSim simulation package to give a good precision both on short-term and long-term scales. The body mass and the volume of the various body tissues change with the age of the simulated individual.
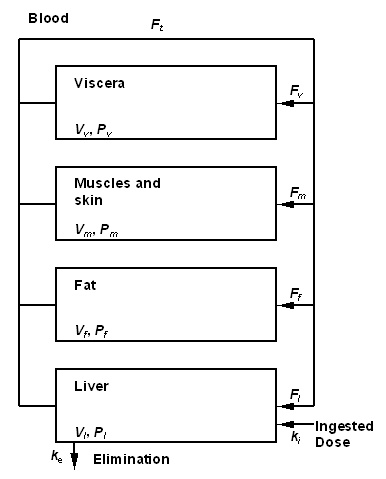
Figure 1 : Toxicokinetic model used to describe TCDD toxicokinetic in the human body[4]. compartments are characterized with volume V and partition coefficient P. Exchanges between are governed by blood flows, F. Elimination is assumed proportional to the elimination constant, ke. The set value of each parameter is given in Table 1. The ingested quantity by unit of time ki (in ng/min), is determined by the exposure scenario.
Figure 1 gives a graphical representation of the model used. Only ingestion exposure is described in this model (the totality of the exposure dose is assumed to be absorbed). The TCDD is supposed to be distributed into different compartments of the body : blood, fat, muscles and skin. The original formulation of van der Molen and coll.[4] regards all these compartments as being with balance in an instantaneous way. This assumption is acceptable only if slow evolutions of absorption are the limiting factor of the kinetics of the product. Since the simulation of a short peak of exposure interests us, we developed a traditional dynamic formulation[5], specifies at the same time on short scales of time and the long-term.
Model equations Equations defining the proposed model are the following : For quantites of TCDD in fat, viscera, muscle and skin, and liver : (1) (2) (3) (4) La concentration artérielle est calculée par : (5)
The cardiac output, Ft, is proportinal to the ventilation rate, Fp : (1) The body volume evolve as a function of age : (6) The volume of fat, viscera, liver also evolve as a function of age[4]: (7) (8) (9) Volume of "muscles and skin" compartment is calculated as the difference between 90% of the total body volume (because bones are not included) and the other compartments : (10) Units used are : quantities of TCDD are expressed in ng, TCDD concentrations in ng/L, age in years volumes in liter, flows in L/min, the elimination constant in min-1, the ingested quantity by unit of time in ng/min. The body density is assumed equal to 1.
Figure 2 presents the temporal evolution of these parameters for a woman (the evolution is overall similar for a man). The reference averaged values used for the parameters not evolving with time are given in Table 1. The equations of the model were coded using the MCSim software[6].
Figure 2 : Temporal evolution of volumes for the woman[4].
- Applications examples
Example of the use of this model can be found in the paper by Bois[7]
Model inputs
All intakes are given in ng/min. A typical unit is pg/d; to change from the latter to the former, divide by 1440000.
Background exposure parameters:
- dose1: intake of dioxin during age 0 - 5 years
- dose2: intake of dioxin during age 5 - 10 years
- dose3: intake of dioxin during age 10 -15 years
- dose4: intake of dioxin during age 15 - 40 years
- dose5: intake of dioxin during age 40 - years
Peak exposure parameters (in addition to the background)
- peakstart: start of the peak exposure period (in days of age)
- peakend: end of the peak exposure period (in days of age)
- peakdose: Additional intake of dioxin during the peak period (in ng/min)
This model relates to physiologically based toxicokinetics modelling process. The presented PBTK model allows to simulate ingestion exposures to 2,3,7,8-tétra-chloro-p-dioxin (TCDD) for a woman over her whole life. The model computes various measures of internal dose as a function of time. The superposition of a peak exposure to a time-varying background intake can be described. The model equations are solved dynamically (by numerical integration) with the MCSim simulation package to give a good precision both on short-term and long-term scales. The body mass and the volume of the various body tissues change with the age of the simulated individual.
Model description
- Purpose
This model relates to physiologically based toxicokinetics modelling process. The presented PBTK model allows to simulate ingestion exposures to 2,3,7,8-tétra-chloro-p-dioxin (TCDD) for a woman over her whole life. TCDD is a persistent chemical found in trace amounts all over the globe. It accumulates in animal fat all along the trophic chain. Human exposure to TCDD is therefore almost unavoidable, even if in trace amounts. TCDD has multiple effects on health.
- Boundaries
It is related to woman exposure through food.
- Input
Input data have to be written directly on the webpage. Data consist in: background rates, for different periods of life, beginning, end and level of peak exposure.
- Output
Output data are the concentrations in different parts of the body (blood, liver, fat, well-perfused tissues and poorly-perfused tissues) as a function of time.
Description of processes modelled and of technical details
Figure 1 : Toxicokinetic model used to describe TCDD toxicokinetic in the human body (d'après (Van der Molen et al. 1996)). compartments are characterized with volume V and partition coefficient P. Exchanges between are governed by blood flows, F. Elimination is assumed proportional to the elimination constant, ke. The set value of each parameter is given in Table 1. The ingested quantity by unit of time ki (en ng/min), is determined by the exposure scenario.
| Parameter(a) | Symbol | Numerical Value |
|---|---|---|
| Ventilation rate | Fp | 8,0 |
| Blood over air ventilation rate | R | 1,14 |
| Blood flow rates | ||
| Fat | Ff | 0,09 |
| Liver | Fl | 0,24 |
| Muscles and skin | fm | 0,18 |
| Viscera | fv | – (b) |
| Volumes | ||
| Total body volume | Vt | – (c) |
| Fat | Vf | – (c) |
| Liver | Vl | – (c) |
| Muscles and skin | Vm | – (c) |
| Viscera | Vv | – (c) |
| Partition Coefficient | ||
| Fat | Pf | 300 |
| Liver | Pl | 25 |
| Muscles and skin | Pm | 4 |
| Viscera | Pv | 10 |
| Elimination constant | ke | 8,45´;10-8 (d) |
- (a) Units : volumes (L), blood flow (L/min), et elimination constant (min-1).
- (b) Blood flow rate to viscera is calculated by difference between 1 and the sum of blood flow rates toward the other compartments.
- (c) Volumes evolve with time.
- (d) Corresponds to a half-life of 15,6 years.
Figure 1 gives a graphical representation of the model used. Only ingestion exposure is described in this model (the totality of the exposure dose is assumed to be absorbed). The TCDD is supposed to be distributed into different compartments of the body : blood, fat, muscles and skin. The original formulation of van der Molen and coll. (Van der Mollen et al. 1996) regards all these compartments as being with balance in an instantaneous way. This assumption is acceptable only if slow evolutions of absorption are the limiting factor of the kinetics of the product. Since the simulation of a short peak of exposure interests us, we developed a traditional dynamic formulation (Gerlowski et al. 1983), specifies at the same time on short scales of time and the long-term.
Model equations
Equations defining the proposed model are the following:
For quantities of TCDD in fat, viscera, muscle and skin, and liver:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta Q_f}{\delta t} = f_f \cdot F_t \Bigl( C_{art} - \frac{Q_f}{V_f \times P_f} \Bigr) \qquad (1) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta Q_v}{\delta t} = f_v \cdot F_t \Bigl( C_{art} - \frac{Q_v}{V_v\times P_v} \Bigr) \qquad (2) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta Q_m}{\delta t} = f_m \cdot F_t \Bigl( C_{art} - \frac{Q_m}{V_m\times P_m} \Bigr) \qquad (3) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta Q_l}{\delta t} = f_l \cdot F_t \Bigl( C_{art} - \frac{Q_l}{V_l\times P_l} \Bigr) - k_e \times Q_l + k_i \qquad (4) }
The arterial concentration is calculated by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{art} = \Bigl(\frac{f_f \times Q_f}{V_f \times P_f} + \frac{f_v \times Q_v}{V_v \times P_v} + \frac{f_m \times Q_m}{V_m \times P_m} + \frac{f_f \times Q_l}{V_f \times P_l}\Bigr) \qquad (5) }
Cardiac output Ft is proportional to the ventilation rate Fp:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_t = 0.7 \times F_p \times R \qquad (6) }
The body volume evolves as a function of age:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_t = 0.1959 \times t - \frac{57.497}{(1+4.617 \times exp(-0.572 \times (t-11.33)))^{1/4.617}} \qquad (7) }
The volume of fat, viscera, liver also evolve as a function of age (Van der Molen et al. 1996):
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_g = \begin{cases} 0.5+4.5 \times \frac{t}{10}, \qquad\text{if }t\ge 10\text{,}\\ 0.5+4.5+8\times\frac{t-10}{15}, \qquad\text{if }10 \le t \le 15\\0.5+4.5+8+17\times\frac{t-15}{55}, \qquad\text{if }t \ge15\text{.}\end{cases} \qquad (8) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_v = \frac{6.095}{(1+4.617 \times exp(-0.3937 \times (t-6.5582)))^{1/4.617}} \qquad (9) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_f = \frac{1.758}{(1+4.617 \times exp(-0.3309 \times (t-12.478)))^{1/4.617}} \qquad (10) }
Volume of "muscles and skin" compartment is calculated as the difference between 90% of the total body volume (because bones are not included) and the other compartments:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_m = 0.9 \times V_t - V_f - V_v - V_l \qquad (11) }
Units used are : quantities of TCDD are expressed in ng, TCDD concentrations in ng/L, age in years volumes in liter, flows in L/min, the elimination constant in min-1, the ingested quantity by unit of time in ng/min. The body density is assumed equal to 1.
Figure 2 presents the temporal evolution of these parameters for a woman (the evolution is overall similar for a man). The reference averaged values used for the parameters not evolving with time are given in Table 1. The equations of the model were coded using the MCSim software (Bois et al. 1997).
Figure 2 : Temporal evolution of volumes for the woman (Van der Molen et al. 1996).
- Rationale
The proposed model is based on a previous one proposed by van der Mollen and colleagues in 1996 (Van der Mollen et al. 1996). The model computes various measures of internal dose as a function of time. The superposition of a peak exposure to a time-varying background intake can be described. All ingested TCDD is supposed to be absorbed. TCDD is supposed to distribute between blood, fat, muscles and skin, and viscera. The model equations are solved dynamically (by numerical integration) with the MCSim simulation package to give a good precision both on short-term and long-term scales. The body mass and the volume of the various body tissues change with the age of the simulated individual.
- See also
- Contact person: Frédéric Y. Bois (frederic.bois [at] ineris.fr
- Time required for a typical run: Typically one second
- Degree of mastery: Basic user / Expert user
- Intellectual property rights (who is allowed to access or use the model?): Free software.
- Tool website: [3] and [4]
See also
References
- ↑ Aylward LL et al. (2005a) Concentration-dependent TCDD eliminationi kinetics in humans: toxicokinetic modeling for moderately to highly exposed adults from Seveso, Italy, and Vienna, Austria, and impact on dose estimates for the NIOSH cohort. Journal of Exposure Analysis and Environmental Epidemiology 15: 51-65.
- ↑ Aylward LL et al. (200b) Exposure reconstruction for the TCDD-exposed NIOSH cohort using a concentration- and age-dependent model of elimination. Risk Analysis 25: 4: 945-956.
- ↑ http://toxi.ineris.fr/activites/toxicologie_quantitative/toxicocinetique/modeles/dioxine/sub_dioxine.php
- ↑ 4.0 4.1 4.2 4.3 4.4 Van der Molen, G. W., S. A. L. M. Kooijman and W. Slob (1996). "A generic toxicokinetic model for persistent lipophilic compounds in humans: an application to TCDD." Fundamental and Applied Toxicology 31: 83-94.
- ↑ Gerlowski, L. E. and R. K. Jain (1983). "Physiologically based pharmacokinetic modeling: principles and applications." Journal of Pharmaceutical Sciences 72: 1103-1127.
- ↑ Bois, F. Y. and D. Maszle (1997). "MCSim: a simulation program." Journal of Statistical Software 2(9): [1].
- ↑ Bois, F. Y. (2003). "Modélisation toxicocinétique de la concentration sanguine de 2,3,7,8-tetrachloro-p-dioxine après ingestion chez la femme." Environnement, Risques et Santé 2(1). [Toxicokinetic modelling of 2,3,7,8-tétrachloro-p-dioxin blood concentration after ingestion by women. Environnement, Risque et Santé, (2003) 2:45-53. ]
- Bois, F. Y. (2003). "Modélisation toxicocinétique de la concentration sanguine de 2,3,7,8-tetrachloro-p-dioxine après ingestion chez la femme." Environnement, Risques et Santé 2(1).
- Bois, F. Y. and D. Maszle (1997). "MCSim: a simulation program." Journal of Statistical Software 2(9)
- Gerlowski, L. E. and R. K. Jain (1983). "Physiologically based pharmacokinetic modeling: principles and applications." Journal of Pharmaceutical Sciences 72: 1103-1127.
- Van der Molen, G. W., S. A. L. M. Kooijman and W. Slob (1996). "A generic toxicokinetic model for persistent lipophilic compounds in humans: an application to TCDD." Fundamental and Applied Toxicology 31: 83-94.
- Van der Molen GW, Kooijman BALM, Wittsiepe J, et al. Estimation of dioxin and furan elimination rates with a pharmacokinetic model. JOURNAL OF EXPOSURE ANALYSIS AND ENVIRONMENTAL EPIDEMIOLOGY 10 (6): 579-585 Part 1 NOV-DEC 2000.
- Van der Molen GW, Kooijman SALM, Michalek JE, et al. The estimation of elimination rates of persistent compounds: A re-analysis of 2,3,7,8-tetrachlorodibenzo-p-dioxin levels in Vietnam veterans CHEMOSPHERE 37 (9-12): 1833-1844 OCT-NOV 1998.