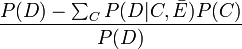Attributable risk

**Progression class**
In Opasnet many pages being worked on and are in different classes of progression. Thus the information on those pages should be regarded with consideration. The progression class of this page has been assessed: This page is a full draft This page has been written through once, so all important content is already where it should be. However, the content has not been thoroughly checked yet, and for example important references might still be missing.	The content and quality of this page is/was being curated by the project that produced the page.

This page is a knowledge crystal of subtype method. The page identifier is Op_en6211
Moderator:Jouni (see all)

Upload data {{#opasnet_base_link:Op_en6211}}

Attributable risk is a fraction of total risk that can be attributed to a particular cause. There are a few different ways to calculate it. Population attributable fraction of an exposure agent is the fraction of disease that would disappear if the exposure to that agent would disappear in a population. Etiologic fraction is the fraction of cases that have occurred earlier than they would have occurred (if at all) without exposure. Etiologic fracion cannot typically be calculated based on risk ratio (RR) alone, but it requires knowledge about biological mechanisms.

Question

How to calculate attributable risk? What different approaches are there, and what are their differences in interpretation and use?

Answer

Risk ratio (RR)

risk among the exposed divided by the risk among the unexposed

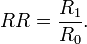
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle RR = \frac{R_1}{R_0}.}

Excess fraction

(sometimes called attributable fraction) the fraction of cases among the exposed that would not have occurred if the exposure would not have taken place:

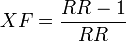
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XF = \frac{RR - 1}{RR}}

Population attributable fraction

the fraction of cases among the total population that would not have occurred if the exposure would not have taken place. The most useful formulas are

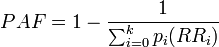
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = 1 - \frac{1}{\sum_{i=0}^k p_i (RR_i)}}

for use with several population subgroups (typically with different exposure levels). Not valid when confounding exists. Subscript i refers to the i^th subgroup. p_i = proportion of total population in i^th subgroup.

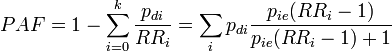
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = 1- \sum_{i=0}^k \frac{p_{di}}{RR_i} = \sum_i p_{di} \frac{p_{ie}(RR_i - 1)}{p_{ie}(RR_i - 1) + 1}}

which produces valid estimates when confounding exists but with a problem that parameters are often not known. p_di is the proportion of cases falling in subgroup i (so that Σ_ip_di = 1), p_ie is the proportion of exposed people within subgroup i (and 1-p_ie is the fraction of unexposed)

Etiologic fraction

Fraction of cases among the exposed that would have occurred later (if at all) if the exposure had not taken place. It cannot be calculated without understanding of the biological mechanism, but there are equations for several specific cases. If survival functions are known, the lower limit of EF can be calculated:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_G [f_1(u) - f_0(u)]\mathrm{d}u / [1 - S_1(t)],}

where 1 means the exposed group, 0 means the unexposed group, f is the proportion of population dying at particular time points, S is the survival function (and thus f(u) = -dS(u)/du), t is the length of the observation time, u the observation time and G is the set of all u < t such that f₁(u) > f₀(u).

In a specific case where the survival distribution is exponential, the following formula can be used for the lowest possible EF. However, the exponential survival model says nothing about which individuals are affected and lose how much life years, and therefore in this model the actual EF may be between the lower bound and 1.

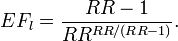
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EF_l = \frac{RR - 1}{RR^{RR/(RR-1)}}.}

Finally, it should be remembered that if the rank preserving assumption holds (i.e. the rank of individual deaths is not affected by exposure: everyone dies in the same order as without exposure, just sooner), the EF can be as high as 1.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EF_u = 1}

With this code, you can compare excess fraction and lower (assuming exponential survival distribution) and upper bounds of etiological fraction.

+ Show code - Hide code

library(OpasnetUtils)
library(psych)
AF <- function(x) {return(data.frame(RR = x, XF = (x-1)/x, EF_exp_lower = (x-1)/x^(x/(x-1)), EF_upper = 1))}

oprint(AF(RR))

This code creates a simulated population of 200 individuals that are now 60 years of age. It calculates their survival and excess and etiologic fractions in different mechanistic settings. Relative risk of 1.2 and a constant hazard rate will be applied in all scenarios.

+ Show code - Hide code


#This is code 6211/ on page [[Attributable risk]]
library(OpasnetUtils)
library(reshape2)
library(ggplot2)

cat("Analysis of variation in etiologic fraction. Parameters:\n")
if(linear) cat("Uniform survival distribution (people die between 60 and 80 years)\n") else
  cat("Exponential survival distribution (remaining life expectancy at 60 year is 10 years\n")
if(shuffle == 1) {
  cat("Preserve rank order of individual lifetimes\n")
} else {
  if(shuffle == 2) {
    cat("Minimize EF by accumulating life loss to the hardy\n")
  } else {
    cat("Shuffle lifetimes with approximate rank correlation\n")
  }
}

#linear <- TRUE
#scenario <- c(1, 2, 3)
#crr <- NULL
RR. <- 1.2

objects.latest("Op_en6007", code_name = "answer") # Fetch correlvar

lifetime <- data.frame(
  Unexposed = if(linear) seq(0, 20, 0.1) else qexp((1:200)/201, 1/10)
)

yll <- mean(lifetime$Unexposed) * (RR. - 1) / RR.

if(1 %in% scenario) {
  lifetime$ConstantSurvShift <- lifetime$Unexposed - yll
}
#if(2 %in% scenario) {
#  sequ <- RR. / (RR. - 1)
#  temp <- round(1:(nrow(lifetime) / sequ) * sequ)
#  lifetime$AFdistribution <- lifetime$Unexposed
#  lifetime$AFdistribution[temp] <- lifetime$Unexposed[temp] - yll * sequ
#}

if(2 %in% scenario) {
  lifetime$CompetingCauses <- if(linear) {
    seq(0, by = 0.1/RR., length.out = nrow(lifetime))
  } else {
    qexp((1:200)/201, 1/10*RR.)
  }
}

cat("Individual lifetimes in the population when order is preserved.\n")
oprint(lifetime)

# Minimize EF by sorting

if(shuffle == 2) {
  for(j in colnames(lifetime)[!colnames(lifetime) %in% c("Id", "Unexposed")]) {
    for(i in 1:nrow(lifetime)) {
      pos <- match(TRUE, lifetime$Unexposed[i] <= lifetime[i:nrow(lifetime) , j]) + i - 1
      if(pos > i & !is.na(pos)) {
        block1 <- if(i < 2) numeric() else 1:(i - 1)
        block2 <- if(pos == nrow(lifetime)) numeric() else (pos+1):nrow(lifetime)
        temp <- c(block1, pos, i:(pos-1), block2)
        if(length(temp) == nrow(lifetime)) {
          lifetime[[j]] <- lifetime[temp , j]
        } else {
          warning("Vectors do not match: i ", i, ", pos ", pos, ", temp ", temp)
        }
      }
    }
  }
  cat("Individual lifetimes in the population when life loss is accumulated to the hardy.\n")
  oprint(lifetime)
}

# Shuffle individuals in different scenarios

if(shuffle == 3) {
  Sigma <- matrix(crr, nrow = ncol(lifetime), ncol = ncol(lifetime)) + diag(ncol(lifetime))*(1 - crr)
  lifetime <- correlvar(lifetime, Sigma)
  lifetime <- lifetime[order(lifetime$Unexposed) , ]

  for(j in colnames(lifetime)[colnames(lifetime) != "Unexposed"]) {
    for(i in order(lifetime[[j]], decreasing = TRUE)) {
      pos <- match(TRUE, lifetime[i,j] <= lifetime$Unexposed)
      if(pos > i & !is.na(pos)) {
        block1 <- if(i < 2) numeric() else 1:(i - 1)
        block2 <- if(pos == nrow(lifetime)) numeric() else (pos+1):nrow(lifetime)
        temp <- c(block1, (i+1):pos, i, block2)
        if(length(temp) == nrow(lifetime)) {
          lifetime[[j]] <- lifetime[temp , j]
        } else {
          warning("Vectors do not match: i ", i, ", pos ", pos, ", temp ", temp)
        }
      }
    }
  }
}

cat("Rank correlation coefficients.\n")
oprint(cor(lifetime, method = "spearman"))

plot(lifetime)

lifetime$Id <- 1:nrow(lifetime)
objects.latest("Op_en6211", code_name = "EF")

RR <- EvalOutput(RR)

cat("Relative risks observed in the model.\n")
oprint(RR@output)

lif <- lif + 60 
# Only after the RR and le have been calculated, we can start talking about the 
# total life expectancy rather than the remaining life expectancy at 60 a.

metrices <- EvalOutput(metrices)

cat("Different etiologic and attributable fractions.\n")
oprint(unkeep(metrices, sources = TRUE))

oline <- data.frame(A = c(
  min(result(lif)[lif$Scenario == "Unexposed"]),
  max(result(lif)[!lif$Scenario %in% c("Id", "Unexposed")])
))

plotting <- lif[lif$Scenario == "Unexposed" , colnames(lif@output) != "Scenario"]
plotting <- plotting + lif - lif

BS <- 24

ggplot()+geom_point(data = plotting@output, aes(x = lifResult, y = Result, colour = Scenario))+
  geom_line(data = oline, aes(x = A, y = A)) + theme_gray(base_size = BS)+
  labs(
    title = "Scatter plot of individual lifetimes",
    x = "Unexposed (years)",
    y = "Exposed (years)"
  )

ggplot(lif@output, aes(x = Id, y = lifResult, colour = Scenario))+geom_point()+
 theme_gray(base_size = BS) + labs(title = "Life expectancies of 200 individuals", y = "Age at death", x = "Individual")

ggplot(fr@output, aes(x = Time, y = frResult, colour = Scenario, group = Scenario))+
  geom_line() + 
  theme_gray(base_size = BS)+
  theme(axis.text.x = element_text(angle = 90, hjust = 1)) +
  labs(title = "fraction of people dying at different time groups")
  
ggplot(surv@output, aes(x = Time, y = survResult, colour = Scenario, group = Scenario))+geom_line() + 
 theme_gray(base_size = BS) + labs(title = "Survival curves in different scenarios")+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))
  
ggplot(EF_eq9@output, aes(x = Time, y = EF_eq9Result, colour = Scenario, group = Scenario))+geom_line()+
 theme_gray(base_size = BS) + labs(title = "Development of etiologic fraction in time")+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

Rationale

Definitions of terms

There are several different kinds of proportions that sound alike but are not. Therefore, we explain the specific meaning of several terms.

Number of people (N)

The number of people in the total population considered, including cases, non-cases, exposed and unexposed. N₁ and N_o are the numbers of exposed and unexposed people in the population, respectively.

Classifications

There are three classifications, and every person in the total population belongs to exactly one group in each classification.

Disease (D): classes case (c) and non-case (nc)
Exposure (E): classes exposed (1) and unexposed (0)
Population subgroup (S): classes i = 0, 1, 2, ..., k (typically based on different exposure levels)
Confounders (C): other factors correlating with exposure and disease and thus potentially causing bias in estimates unless measured and adjusted for.

Excess fraction (XF): The proportion of exposed cases that would not have occurred without exposure on population level.
Etiologic fraction (EF): The proportion of exposed cases that would have occurred later (if at all) without exposure on individual level.
Hazard fraction (HF): The proportion of hazard rate that would not be there without exposure, HF = [h₁(t) - h₀(t)]/h₁(t) = [R(t) - 1]/R(t), where h(t) is hazard rate at time t and R(t) = h₁(t)/h₀(t).
Attributable fraction (AF): An ambiguous term that has been used for excess fraction, etiologic fraction and hazard fraction without being specific. Therefore, its use is not recommended.
Population attributable fraction (PAF): The proportion of all cases (exposed and unexposed) that would not have occurred without exposure on population level. PAF_i is PAF of subgroup i.
Risk of disease (hazard rates): R₁ and R₀ are the risks of disease in the exposed and unexposed group, respectively, and RR = R₁ / R₀. RR_i = relative risk comparing i^th exposure level with unexposed group (i = 0). Note that often texts are not clear when they talk about risk proportion = number of cases / number of population and thus risk ratio; and when about hazard rates = number of cases / observation time and thus rate ratio. RR may mean either one. If occurrence of cases is small, risk ratio and rate ratio approach each other, because then cases hardly shorten the observation time in the population.
Proportion exposed (p_e, p_ie, p_ed): proportion of exposed among the total population or within subgroup i or within cases (we use subscript d as diseased rather than c as cases to distinguish it from subscript e): p_e = N(E=1)/N, p_ie = N(E=1,S=i)/N(S=i), p_ed = N(E=1,D=c)/N(D=c)
Proportion of population (p_i): proportion of population in subgroups i among the total population: N(S=i)/N. p'_i is the fraction of population in a counterfactual ideal situation (where the exposure is typically lower).
Proportion of cases of the disease (p_di): proportion of cases in subgroups i among the total cases: N(D=c,S=i)/N(D=c) (so that Σ_ip_di = 1).

Excess fraction

Rockhill et al.^[1] give an extensive description about different ways to calculate excess fraction (XF) and population attributable fraction (PAF) and assumptions needed in each approach. Modern Epidemiology ^[2] is the authoritative source of epidemiology. They first define excess fraction XF for a cohort of people (pages 295-297). It is the fraction of cases among the exposed that would not have occurred if the exposure would not have taken place.R↻ However, both sources use the term attributable fraction rather than excess fraction.

Impact of confounders

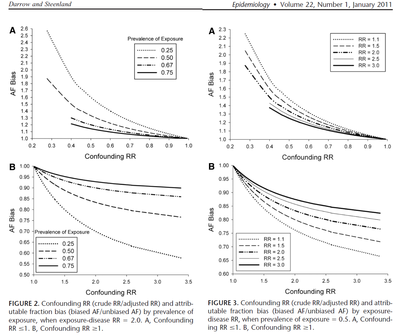
The problem with the two PAF equations (see Answer) is that the former has easier-to-collect input, but it is not valid if there is confounding. It is still often mistakenly used. The latter equation would produce an unbiased estimate, but the data needed is harder to collect. Darrow and Steenland^[3] have studied the impact of confounding on the bias in attributable fraction. This is their summary:

**The impact of confounding on the bias in excess fraction.**
Bias in excess fraction	Confounding in RR	Confounding in inputs
AF bias (-), calculated AF is smaller than true AF	Conf RR (+), crude RR is larger than adjusted (true) RR	Confounder is positively associated with exposure and disease (++)
AF bias (-), calculated AF is smaller than true AF	Conf RR (+), crude RR is larger than adjusted (true) RR	Confounder is negatively associated with exposure and disease (--)
AF bias (+), calculated AF is larger than true AF	Conf RR (-), crude RR is smaller than adjusted (true) RR	Confounder is negatively associated with exposure and positively with disease (-+)
AF bias (+), calculated AF is larger than true AF	Conf RR (-), crude RR is smaller than adjusted (true) RR	Confounder is positively associated with exposure and negatively with disease (+-)

Population attributable fraction

The population attributable fraction PAF is the fraction of all cases (exposed and unexposed) that would not have occurred if the exposure had been absent.

**Different ways to calculate population attributable fraction PAF.**
#	Formula	Description
1	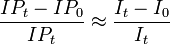Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{IP_t - IP_0}{IP_t} \approx \frac{I_t - I_0}{I_t}}	is empirical approximation of ^[1] Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{P(D) - \sum_C P(D\|C, \bar{E}) P(C)}{P(D)}} where IP₁ = cumulative proportion of total population developing disease over specified interval; IP₀ = cumulative proportion of unexposed persons who develop disease over interval, C means other confounders, and E is exposure and a bar above E means no exposure. Valid only when no confounding of exposure(s) of interest exists. If disease is rare over time interval, ratio of average incidence rates I₀/I_t approximates ratio of cumulative incidence proportions, and thus formula can be written as (I_t - I₀)I_t. Both formulations found in many widely used epidemiology textbooks. ⇤--#: . Is there an error in the text about the approximation? --Jouni (talk) 10:05, 28 June 2016 (UTC) (type: truth; paradigms: science: attack)
2	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{p_e(RR-1)}{p_e(RR-1)+1}}	Transformation of formula 1.^[1] Not valid when there is confounding of exposure-disease association. RR may be ratio of two cumulative incidence proportions (risk ratio), two (average) incidence rates (rate ratio), or an approximation of one of these ratios. Found in many widely used epidemiology texts, but often with no warning about invalidness when confounding exists.
3	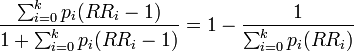Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sum_{i=0}^k p_i (RR_i - 1)}{1 + \sum_{i=0}^k p_i (RR_i - 1)} = 1 - \frac{1}{\sum_{i=0}^k p_i (RR_i)}}	Extension of formula 2 for use with multicategory exposures. Not valid when confounding exists. Subscript i refers to the i^th exposure level. Derived by Walter^[4]; given in Kleinbaum et al.^[5] but not in other widely used epidemiology texts.
4	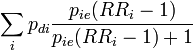Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_i p_{di} \frac{p_{ie}(RR_i - 1)}{p_{ie}(RR_i - 1) + 1}}	A useful formulation from^[3]. Note that RR_i is the risk ratio for subgroup i due to the subgroup-specific exposure level and assumes that everyone in that subgroup is exposed to that level or none.
5	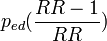Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{ed}(\frac{RR-1}{RR})}	Alternative expression of formula 3.^[1] Produces internally valid estimate when confounding exists and when, as a result, adjusted relative risks must be used.^[6] In Kleinbaum et al.^[5] and Schlesselman.^[7]
6	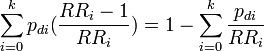Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^k p_{di} (\frac{RR_i - 1}{RR_i}) = 1- \sum_{i=0}^k \frac{p_{di}}{RR_i}}	Extension of formula 5 for use with multicategory exposures.^[1] Produces internally valid estimate when confounding exists and when, as a result, adjusted relative risks must be used. See Bruzzi et al. ^[8] and Miettinen^[6] for discussion and derivations; in Kleinbaum et al.^[5] and Schlesselman.^[7]

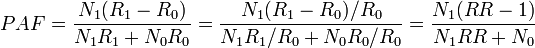
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \frac{N_1 (R_1 - R_0)}{N_1 R_1 + N_0 R_0} = \frac{N_1 (R_1 - R_0)/R_0}{N_1 R_1/R_0 + N_0 R_0/R_0} = \frac{N_1 (RR - 1)}{N_1 RR + N_0}}

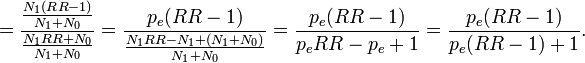
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{ \frac{N_1 (RR - 1)}{N_1 + N_0} }{ \frac{N_1 RR + N_0}{N_1 + N_0}} = \frac{ p_e (RR - 1) }{ \frac{N_1 RR - N_1 + (N_1 + N_0)}{N_1 + N_0}} = \frac{p_e (RR - 1)}{p_e RR - p_e + 1} = \frac{p_e (RR - 1)}{p_e (RR - 1) + 1}.}

Note that there is a typo in the Modern Epidemiology book: the denominator should be p(RR-1)+1, not p(RR-1)-1.

Population attributable fraction can be calculated as a weighted average based on subgroup data:

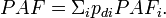
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \Sigma_i p_{di} PAF_{i}.}

Specifically, we can divide the cohort into subgroups based on exposure (in the simplest case exposed and unexposed), so we get

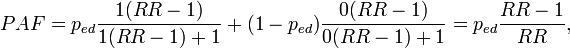
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = p_{ed} \frac{1(RR - 1)}{1(RR - 1) + 1} + (1 - p_{ed}) \frac{0(RR - 1)}{0(RR - 1) +1} = p_{ed} \frac{RR - 1}{RR},}

where p_c is the proportion of cases in the exposed group among all cases; this is the same as exposure prevalence among cases.

WHO approach

According to WHO, PAF is ^[9]

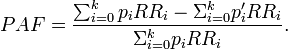
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \frac{\sum_{i=0}^k p_i RR_i - \Sigma_{i=0}^k p'_i RR_i}{\Sigma_{i=0}^k p_i RR_i}.}

We can see that this reduces to PAF equation 2 when we limit our examination to a situation where there are only two population groups, one exposed to background level (with relative risk 1) and the other exposed to a higher level (with relative risk RR). In the counterfactual situation nobody is exposed. in this specific case, p_i = p_e. Thus, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \frac{(p_e RR + (1-p_e)*1) - (0*RR + 1*1)}{p_e RR + (1-p_e)*1}}

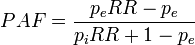
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \frac{p_e RR - p_e}{p_i RR + 1 - p_e}}

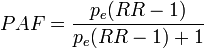
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PAF = \frac{p_e(RR - 1)}{p_e(RR -1) + 1}}

----#: . Constant background assumption section was archived because it was only relevant for a previous HIA model version. --Jouni (talk) 13:17, 25 April 2016 (UTC) (type: truth; paradigms: science: comment)

Etiologic fraction

Etiologic fraction (EF) is defined as the fraction of cases that are advanced in time because of exposure.^[10]R↻ In other words, those cases would have occurred later (if at all), if there had not been exposure. EF can also be called probability of causation, which has importance in court. It can also be used to calculate premature cases, but that term is ambiguous and sometimes it is used to mean cases that have been substantially advanced in time, in contrast to the harvesting effect where an exposure kills people that would have died anyway within a few days. There has been a heated discussion about harvesting effect related to fine particles. Therefore, sometimes excess fraction is used instead to calculate what they call premature mortality, but unfortunately that practice causes even more confusion.R↻ Therefore, it is important to explicitly explain what is meant by the word premature.

Robins and Greenland^[10] studied the estimability of etiologic fraction. They concluded that observations are not enough to conclude about the precise value of EF, because irrespective of observation, the same amount of observed life years lost may be due to many people losing a short time each, or due to a few losing a long time each. The upper limit in theory is always 1, and the lower bound they estimated by this equation (equation 9 in the article):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_G [f_1(u) - f_0(u)]\mathrm{d}u / [1 - S_1(t)],}

where 1 means the exposed group, 0 means the unexposed group, f is the proportion of population dying at particular time points, S is the survival function (and thus f(u) = -dS(u)/du), t is the length of the observation time, u the observation time and G is the set of all u < t such that f₁(u) > f₀(u).

Although the exact value of etiologic fraction cannot be estimated directly from risk ratio (RR), different models offer equations to estimate EF. It is just important to understand, discuss, and communicate, which of the models most closely represents the actual situation observed. Three models are explained here.R↻

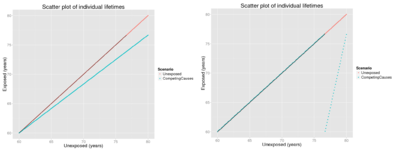
Rank-preserving model says that everyone dies at the same rank order as without exposure, but that the deaths occur earlier. If the exposed population loses life years compared with unexposed population, it is in theory always possible that everyone dies a bit earlier and thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EF_u = 1.}

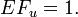
Competing causes model is the most commonly assumed model, but often people do not realise that they make such an assumption. The model says that the exposure of interest and other causes of death are constantly competing, and that the impact of the exposure is relative to the other competing causes. In other words, the hazard rate in the exposed population is h₁(t) = RR h₀(t). Hazard rates are functions of time, and may become very high in very old populations. In any case, the proportional impact of the exposure stays constant.

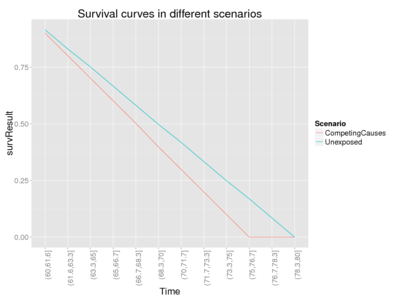
In the case where competing causes model and independence assumtption applies, lower end of EF range is often close to the excess fraction XF. (But it can be lower, as the next example with a skewed exponential distribution demonstrates.)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EF_l = XF = \frac{RR - 1}{RR}.}

Exponential survival model assumes that the hazard rate is constant and the deaths occur following the exponential distribution. Although this model has very elegant formulas, it is typically far from plausible, as the differences in survival may be very large. E.g. with average life expectancy of 70 years, 10 % of the population would die before 8 years of age, while 10 % would live beyond 160 years. In situations where exponential survival model can be used, the lower bound of EF (equation 9^[10]) is as low as

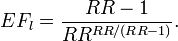
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EF_l = \frac{RR - 1}{RR^{RR/(RR-1)}}.}

For an illustration of the behaviour of EF, see the code "Test different etiologic fractions" in the Answer. Also the true etiologic fraction is calculated for this simulated population, because in the simulation we assume that we know exactly what happens to each individual in each scenario and how much their lengths of lives change. By testing with several inputs, we can see the following pattern (table).

**Different ways to calculate etiologic and excess fractions.**
Equations 9 and 11 refer to Robins and Greenland^[10]. True EF is calculated by comparing individual lifetimes in counterfactual situations in the model. Low means the lower confidence limit.
Survival distribution	Scenario	Excess fraction XF	True etiologic fraction	EF_low from Eq 9	EF_low from Eq 11
Uniform	Competing causes, minimize EF[4]	0.17	0.17	0.17	0.07
Uniform	Competing causes, preserve rank order[5]	0.17	1.00	0.17	0.07
Exponential	Competing causes, minimize EF[6]	0.17	0.07	0.07	0.07
Exponential	Competing causes, preserve rank order[7]	0.17	1.00	0.07	0.07

As we can see from the table, true etiologic fraction can vary substantially - in theory. High values assume that most people are affected by a small life loss. This might be true with causes that worsen general health, thus killing the person a bit earlier than what would have happened if the person had been in a hardier state.

When we compare equations 9 and 11, we can see that the former never performs worse than the latter. This is simply because equation 11 was derived from equation 9 by making an additional assmuption that the survival distribution is exponential. Indeed, in such a case they produce identical values but in other cases equation 11 underestimates EF compared with equation 9. A practical conclusion is that if survival curves for exposed and unexposed groups are available, equation 9 rather than equation 11 should always be used. Even excess fraction is usually a better estimate than an estimate from equation 11, with the exception of exponential survival distribution.

Calculations

⇤--#: . UPDATE AF TO REFLECT THE CURRENT IMPLEMENTATION OF ERF Exposure-response function --Jouni (talk) 05:20, 13 June 2015 (UTC) (type: truth; paradigms: science: attack)

+ Show code - Hide code

# This is code Op_en6211/AF on page [[Attributable risk]]
# Parameters: none

library(OpasnetUtils)

# AF = attributable fraction
# EF = etiologic fraction
# PAF = population attributable fraction using 
EF <- Ovariable("EF", 
	dependencies = data.frame(Name = c(
		"RR" # Risk ratio
	)),
	
	formula = function(...) {

		R <- unkeep(RR, sources = TRUE, prevresults = TRUE)
		EF <- (RR - 1) / R^(R/(R-1))
		EF <- EF * Ovariable("temp", data = data.frame(
			EFestimate = c("Low", "High"),
			Result = 1
		))
		result(EF)[EF$EFestimate == "High"] <- 1

		return(EF)
	}
)

AF <- Ovariable("AF", 
	dependencies = data.frame(Name = c(
		"RR" # Risk ratio
	)),
	
	formula = function(...) {

		AF <- (RR - 1) / unkeep(RR, sources = TRUE, prevresults = TRUE)

		return(AF)
	}
)

PAF <- Ovariable("PAF", 
	dependencies = data.frame(Name = c(
		"RR", # Risk ratio
		"pci", # proportion of cases falling subgroup i among all cases
		"pei" # proportion of exposed people within subgroup i
	)),
	
	formula = function(...) {

		peirri <- pei * (RR - 1)
		peirri <- unkeep(peirri, sources = TRUE, prevresults = TRUE)

		PAF <- pci * peirri / (peirri + 1) # The population subgroup could be summed up.

		return(PAF)
	}
)

objects.store(EF, AF, PAF)
cat("Ovariables EF, AF, PAF stored.\n")

A previous version of code looked at RRs of all exposure agents and summed PAFs up.

Some interesting model runs:

+ Show code - Hide code

#This is code Op_en6211/EF on page [[Attributable risk]]

library(OpasnetUtils)

lif <- Ovariable(
  "lif",
  dependencies = data.frame(Name = "lifetime"),
  formula = function(...) {
    out <- melt(
       lifetime, 
       id.vars = "Id", 
       value.name = "Result", 
       variable.name = "Scenario"
    )
    out <- Ovariable(
      output = out, 
      marginal = c(TRUE, TRUE, FALSE)
    )
    return(out)
  }
)

le <- Ovariable(
  "le",
  dependencies = data.frame(Name = "lif"),
  formula = function(...) {
    le <- oapply(lif, INDEX = "Scenario", FUN = sum) / 
    oapply(lif, INDEX = "Scenario", FUN = length)
    return(le)
  }
)

RR <- Ovariable(
  "RR",
  dependencies = data.frame(Name = "le"),
  formula = function(...) {
    RR <- le[le$Scenario == "Unexposed" , ]
    RR <- unkeep(RR, cols = c("Scenario", "lifResult"))
    RR <- RR / le
    RR <- unkeep(RR, prevresults = TRUE)
    return(RR)
  }
)

fr <- Ovariable("fr", 
  dependencies = data.frame(
    Name = "lif"
  ),
  formula = function(...) {
    out <- lif
    temp2 <- cut(result(out), breaks = 12)
    out$Time <- temp2
    out <- out * 0 + 1/oapply(out, cols = c("Id", "Time"), FUN = length)
    temp <- Ovariable(
      "temp", 
      data = data.frame(
        Time = levels(temp2),
        Result = 0
      )
    )
    out <- combine(EvalOutput(temp), out)
    out <- oapply(out, cols = "Id", FUN = sum) # Automatic fillna is OK.
    return(out)
  }
)

surv <- Ovariable(
  "surv",
  dependencies = data.frame(Name = "fr"),
  formula = function(...) {
    out <- fr[order(fr$Time) , ]
    temp <- data.frame()
    for(i in unique(out$Scenario)) {
      temp2 <- out[out$Scenario == i , ]
      result(temp2) <- 1 - cumsum(result(temp2))
      temp <- rbind(temp, temp2@output)
    }
    out@output <- temp
    return(out)
  }
)

EF_eq9 <- Ovariable(
  "EF_eq9",
  dependencies = data.frame(Name = c("fr", "surv")),
  formula = function(...) {
    BAU <- fr[fr$Scenario == "Unexposed" , ]
    BAU <- unkeep(BAU, prevresults = TRUE, sources = TRUE, cols = "Scenario")
    
    out <- fr
    result(out) <- pmax(0, result(out - BAU))
    
    out <- out[order(out$Time) , ]
    temp <- data.frame()
    for(i in unique(out$Scenario)) {
      temp2 <- out[out$Scenario == i , ]
      result(temp2) <- cumsum(result(temp2))
      temp <- rbind(temp, temp2@output)
    }
    out@output <- temp
    out <- out / (1 - surv)
    
    return(out)
  }
)

EF_true <- Ovariable(
  "EF_true", 
  dependencies = data.frame(Name = "lif"),
  formula = function(...) {
    BAU <- lif[lif$Scenario == "Unexposed" , ]
    BAU <- unkeep(BAU, cols = "Scenario", prevresults = TRUE, sources = TRUE)
    out <- lif < BAU
    out <- oapply(out, cols = "Id", FUN = sum) / 
      oapply(out, cols = "Id", FUN = length)
    
    return(out)
  }
)

metrices <- Ovariable(
  "metrices", 
  dependencies = data.frame(Name = c("RR", "lif", "EF_true", "EF_eq9")),
  formula = function(...) {
    out <- (RR - 1) / RR
    out$Metric <- "Attributable fraction"
    temp <- (RR - 1)/(RR^(RR/(RR-1)))
    temp$Metric <- "EF_low from eq 11"
    out <- combine(out, temp)
#    result(temp) <- 1
#    temp$Metric <- "EF_up theoretical"
#    out <- combine(out, temp)
    temp <- unkeep(EF_true, sources = TRUE, prevresults = TRUE)
    temp$Metric <- "EF_true"
    out <- combine(out, temp)
    temp <- unkeep(EF_eq9[EF_eq9$Time == levels(EF_eq9$Time)[length(levels(EF_eq9$Time))] , ],
           cols = "Time", sources = TRUE, prevresults = TRUE
    )
    temp$Metric <- "EF_low from Eq 9"
    out <- combine(out, temp)
    

    return(out)
  }
)

objects.store(lif, le, RR, fr, surv, EF_eq9, EF_true, metrices)
cat("Ovariables lif, le, RR, fr, surv, EF_eq9, EF_true, metrices stored.\n")

Demonstration of hazard fractions, survival, and age at death

Figure for manuscript Morfeld, Erren, Hammit etc.

+ Show code - Hide code

library(ggplot2)
library(reshape2)

# Data from https://www.ssa.gov/oact/STATS/table4c6.html

h1 <- c( # Probability of dying per year by age (0-119 years)
	0.006322,
	0.000396,
	0.000282,
	0.000212,
	0.000186,
	0.000162,
	0.000144,
	0.000129,
	0.000114,
	0.0001,
	0.000093,
	0.000101,
	0.000136,
	0.000205,
	0.000299,
	0.000401,
	0.000505,
	0.00062,
	0.000747,
	0.000879,
	0.001019,
	0.001151,
	0.001252,
	0.001309,
	0.001335,
	0.001349,
	0.001369,
	0.001391,
	0.001422,
	0.001459,
	0.001498,
	0.001536,
	0.001576,
	0.001616,
	0.001661,
	0.001716,
	0.001782,
	0.001854,
	0.001931,
	0.002018,
	0.002123,
	0.002252,
	0.002413,
	0.002611,
	0.002845,
	0.003109,
	0.003402,
	0.003736,
	0.004114,
	0.004533,
	0.004987,
	0.005473,
	0.005997,
	0.00656,
	0.007159,
	0.007803,
	0.00848,
	0.00917,
	0.009863,
	0.010572,
	0.011354,
	0.012202,
	0.013061,
	0.01392,
	0.014819,
	0.015826,
	0.016986,
	0.018295,
	0.019776,
	0.021448,
	0.02338,
	0.025549,
	0.027885,
	0.030374,
	0.033099,
	0.036254,
	0.039882,
	0.043879,
	0.048256,
	0.053123,
	0.058711,
	0.065081,
	0.072139,
	0.079912,
	0.088529,
	0.098148,
	0.108902,
	0.120886,
	0.134149,
	0.148699,
	0.164525,
	0.1816,
	0.199884,
	0.219331,
	0.239886,
	0.260269,
	0.280109,
	0.299013,
	0.316578,
	0.332406,
	0.349027,
	0.366478,
	0.384802,
	0.404042,
	0.424244,
	0.445456,
	0.467729,
	0.491116,
	0.515671,
	0.541455,
	0.568528,
	0.596954,
	0.626802,
	0.658142,
	0.691049,
	0.725602,
	0.761882,
	0.799976,
	0.839975,
	0.881973
)
h0 <- h1/1.5
df <- data.frame(
	Age = 0:119,
	h1 = h1,
	h0 = h0,
	S1 = exp(-cumsum(h1)),
	S0 = exp(-cumsum(h0))
)
df$f1 <- df$h1 * df$S1
df$f0 <- df$h0 * df$S0
dfm <- melt(df, id.var="Age")
dfm$Exposure <- ifelse(as.numeric(substr(dfm$variable,2,2)), "Exposed","Nonexposed")
dfm$Parameter <- substr(dfm$variable,1,1)
dfm$Parameter <- factor(
	dfm$Parameter, 
	levels=c("h","S", "f"), 
	labels=c("Hazard rate h (P/year)","Survival S (P)","Age at death f (pd)")
)

pdf("//cesium/jtue$/_Documents/Survivalfunctions.pdf", height=14,width=10.5)
ggplot(dfm, aes(x=Age, y=value, linetype=Exposure))+geom_line(size=1)+
	facet_grid(Parameter~., scales="free_y")+
	labs(y="Probability (P) or probability density (pd)")+
	theme_bw(base_size=24)+theme(legend.position="bottom")
dev.off()

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 Rockhill B, Newman B, Weinberg C. use and misuse of population attributable fractions. American Journal of Public Health 1998: 88 (1) 15-19.[1]
↑ Kenneth J. Rothman, Sander Greenland, Timothy L. Lash: Modern Epidemiology. Lippincott Williams & Wilkins, 2008. 758 pages.
↑ ^3.0 ^3.1 ^3.2 Darrow LA, Steenland NK. Confounding and bias in the attributable fraction. Epidemiology 2011: 22 (1): 53-58. [2] doi:10.1097/EDE.0b013e3181fce49b
↑ Walter SD. The estimation and interpretation of attributable fraction in health research. Biometrics. 1976;32:829-849.
↑ ^5.0 ^5.1 ^5.2 Kleinbaum DG, Kupper LL, Morgenstem H. Epidemiologic Research. Belmont, Calif: Lifetime Learning Publications; 1982:163.
↑ ^6.0 ^6.1 Miettinen 0. Proportion of disease caused or prevented by a given exposure, trait, or intervention. Am JEpidemiol. 1974;99:325-332.
↑ ^7.0 ^7.1 Schlesselman JJ. Case-Control Studies: Design, Conduct, Analysis. New York, NY: Oxford University Press Inc; 1982.
↑ Bruzzi P, Green SB, Byar DP, Brinton LA, Schairer C. Estimating the population attributable risk for multiple risk factors using case-control data. Am J Epidemiol. 1985; 122: 904-914.
↑ WHO: Health statistics and health information systems. [3]. Accessed 16 Nov 2013.
↑ ^10.0 ^10.1 ^10.2 ^10.3 Robins JM, Greenland S. Estimability and estimation of excess and etiologic fractions. Statistics in Medicine 1989 (8) 845-859.

[rockhill-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 Rockhill B, Newman B, Weinberg C. use and misuse of population attributable fractions. American Journal of Public Health 1998: 88 (1) 15-19.[1]

[2] Kenneth J. Rothman, Sander Greenland, Timothy L. Lash: Modern Epidemiology. Lippincott Williams & Wilkins, 2008. 758 pages.

[darrow-3] 3.0 ^3.1 ^3.2 Darrow LA, Steenland NK. Confounding and bias in the attributable fraction. Epidemiology 2011: 22 (1): 53-58. [2] doi:10.1097/EDE.0b013e3181fce49b

[walter-4] Walter SD. The estimation and interpretation of attributable fraction in health research. Biometrics. 1976;32:829-849.

[kleinbaum-5] 5.0 ^5.1 ^5.2 Kleinbaum DG, Kupper LL, Morgenstem H. Epidemiologic Research. Belmont, Calif: Lifetime Learning Publications; 1982:163.

[miettinen-6] 6.0 ^6.1 Miettinen 0. Proportion of disease caused or prevented by a given exposure, trait, or intervention. Am JEpidemiol. 1974;99:325-332.

[schlesselman-7] 7.0 ^7.1 Schlesselman JJ. Case-Control Studies: Design, Conduct, Analysis. New York, NY: Oxford University Press Inc; 1982.

[bruzzi-8] Bruzzi P, Green SB, Byar DP, Brinton LA, Schairer C. Estimating the population attributable risk for multiple risk factors using case-control data. Am J Epidemiol. 1985; 122: 904-914.

[9] WHO: Health statistics and health information systems. [3]. Accessed 16 Nov 2013.

[robins-10] 10.0 ^10.1 ^10.2 ^10.3 Robins JM, Greenland S. Estimability and estimation of excess and etiologic fractions. Statistics in Medicine 1989 (8) 845-859.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Attributable risk

Contents

Question

Answer

Rationale

Excess fraction

Impact of confounders

Population attributable fraction

Etiologic fraction

Calculations

See also

References

Navigation menu