Theoretical grid and road network for Europe
| [show] |
|---|
Scope
What is such a practical road network description for Europe that
- does not require detailed data about the real network,
- reflects the most important properties of the real network?
Result
A4 fractile grid
The basic cell is a rectangle with the area of 1 km2, with sides according to the golden ratio
(a/b=b/(a/2) <=> b2=a2/2 <=> b=a/sqrt(2) | a,b >0.
Thus,
a*a/sqrt(2)=1 <=> a=sqrt(sqrt(2)),
and the sides of the basic cell are 1.189 km and 0.841 km.
The basic cell level is called the A24 grid. When each two adjacent cells are merged, a new grid is formed where the cells have the same shape but double the area. This level is called A23, and so on. The level where the whole Europe is in one grid cell is called A0. It is 3444 km wide and 4871 km long. It covers 16.7 million km2, which is close to the actual land area of the EU-27 ## km2.
The road network is built between the cells from top down in a similar way as fractales: more details can be added with the same simple rules as much as needed. The rules are the following.
Each cell has two diagonals crossing the cell from corner to corner. A point that is on the diagonal at 1/3 from the corner is called a core point. When a cell is divided into two, a road is built between the halves. The road locates between two core points so that the road and the line between the halves form a 90 degree angle and that it is connected to the road network built at the upper levels (if any).
At each division, new roads are built as many segments as there were cells before division, and the length of each segment is 1/3 of the length of the cell. Let's call L the length of roads at level N and s0 the length of the cell at level A0. Thus,
s0 = sqrt(sqrt(2))*(sqrt(2)24)*1 km = sqrt(sqrt(2))*212*1 km = sqrt(sqrt(2))*4048 km
LN= 2N-1* 1/3* s0/sqrt(2)N-1 = 1/3* sqrt(2)N-1*s0 | N>0
This creates a road network that goes into any level of detail, and there is a unique road between any two cells.
There is also a need to give names to the cells in a unique way. If we use binary code, the natural way of giving names is to call one half a zero (that half that already has a road, say), and the other half a one. At N=1, there are no roads yet, so we say that north is 0 and south is 1. The first road goes from north to south at the western side of the halves. Therefore, at N=2 north-west is 00, south-east 11, south-west 10 and north-east 01. The number of digits increase as the cells get smaller, but the left digits always refer to the larger-level cell within which the smaller cell lays.
Road segments are named according to the cell within which the segment connects the two halves. The first segment that connects the halves of the entire area is just called R. The roads at level N=2 the road that connects northern quadrants 00 and 01 is called R0 and similarly R1 connects southern quadrants 10 and 11.
The route and the length of the route between two cells is straightforward. If we have cells 010110001 and 01010011, the route is
- R01011000
- R0101100
- R010110
- R01011
- R0101
- R01010
- R010100
- R0101001
Also the route length is simply L8+L7+L6+L5+L4+L5+L6+L7.
The route length is of course longer than what would be in practice, as there is only one route and it is not designed to be the shortest. If all composite vehicles are forced to take this route, it is longer than what a car would take in practice. On the other hand, if we assume that also composite vehicles are able to take as short routes as cars, then we would lose efficiency in trip aggregation. It is not easy to estimate the loss of this efficiency. Therefore we take the disadvantage for composite traffic and hope that the improved performance will outweight the additional driving distance. In addition, it is possible to estimate the additional driving by measuring true and modelled routes between several pairs of randomly selected points.
text below moved here from Intarese wiki
- Composite traffic is a hypothetical, large-scale demand-responsive public transportation.
- It looks like an Airport taxi with several passengers, but the volume is in the order of 100,000 trips per day or more in an urban area.
- First publication based on modelling in Helsinki, Finland [1].
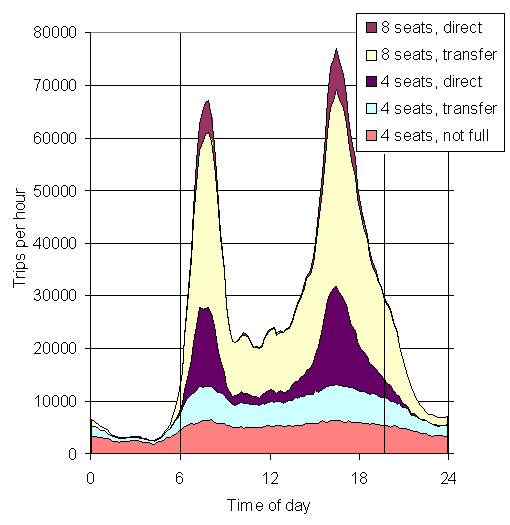
Number of trips in different vehicles
Societal costs with different coverage areas (# of inhabitans in the area)
See also
- Intarese: WP3.1
- An early description of composite traffic (a link to a previous version of this page)
- Congestion charges in a city with composite traffic
- Stakeholder contact information: Composite traffic project (R25) [1]