Bayes (Hierarcical Bayesian model)
| [show] |
|---|
This page describes utilization of Hierarcical Bayesin method. The following page briefly introduces theory behind the method, and illustrates the use the method by examples.
The Bayesian method
The Bayes method is based on the bayesian rule. The following equations can be found from the reference 1, pages 7-8. The Bayesian rule is:
p(θ,y) = p(θ)p(y|θ)
,where p(θ) is prior distribution and on p(y|θ) is distribution acquired from the data. By contidionalizing θ with y (which is known), we get:
p(θ|y) = p(θ)p(y|θ) / p(y)
By conditionalizing this way, we obtain p(?|y), which is prior probability conditionalised by the data. This is also called posterior probability. With these equations, we can adjust presuppositions about the probability density function of the data using data itself. As an end result we obtain upgraded probability density function, which is called posterior density.
Posterior distribution ~ prior distribution x distribution estimated by the data
Hierarcical Bayesian method
We create an example of the method in this article. We study dioxin concentrations in different sea area which we assume to be share a similar form of distribution. In other words, we assume that the concentraions in different areas are samples of the total concentration distribution. Thus, we can use observations of concentrations in all areas to estimate concentrations in one particular area of interest. This means conditionalizing observated values to certain parameters. We assume probabilites to these parameters with new parameters, which are called hyperparameters.
There is an extensive explanation of the idea and the method in reference 1, pages 117-121, and you can find a picture of the method in page 119. In our example, we try to create a model which gives us a relatively accurate concentration estimate for all different areas.
Material and methods
Methods
The method used herein is called hierarcical Bayes method. Theory can be read from reference 1. We used WinBUGS and R as a modelling tool.
http://www.mrc-bsu.cam.ac.uk/bugs/
You can get the program and updates from the address above. They also include quite extensive manuals. You need to copy the text to WinBUGS to a new file, and select decode from tools menu and follow the manual.
Table 1. Names of the variables and parameters in the model.
| Variable | Distribution | Nature | Parameters | Definition | Description |
| alpha.tau | gamma | stocastic | 10^-3 | Parameter of accuracy | |
| alpha.c | norm | stocastic | (0,10^-6) | Mean | |
| alpha0 | calculated | (a.c)-(b.c)*xbar | Starting level | ||
| alpha[i] | norm | stocastic | (a.c,a.t) | Constant term | |
| beta.tau | gamma | stocastic | 10^-3 | Parameter of accuraty for slope | |
| beta.c | norm | stocastic | (0,10^-6) | Mean value of slope | |
| beta[i] | norm | stocastic | (b.c,b.t) | Slope | |
| mu[i,j] | calculated | a[i]+b[i]*(x[j]-xbar) | Estimation for concentration | ||
| x[j] | constant | input | Age categories | ||
| tau.c | gamma | stocastic | 10^-3 | Parameter of accuracy | |
| sigma | calculated | 1/sqrt(tau.c) | Dispersion term | ||
| y[i,j] | norm | stocastic | (mu[i,j],tau.c) | Estimate for concentration without observation |
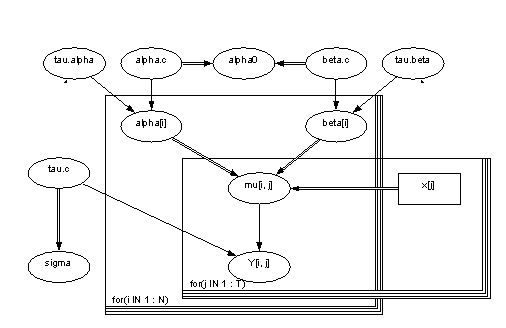
Picture 1. Picture of the model in Win BUGS
Material
The data we used in our example consists of dioxin concentration of herring with ages, sizes and location
We create a model similar to example model in WinBUGS. Variables are analogous as demonstrated below: Variables:
Weight of rat = Concentration of herring Age of rat = Age of herring Number of rat (specimen #) = Location
We ran the model with Win BUGS with herring data, and examined the distribution of variables of interest.In rat example the model estimates distributions for weight for each rat. In our model we estimate concentration distributions for each location.
Results
Descriptive statistics
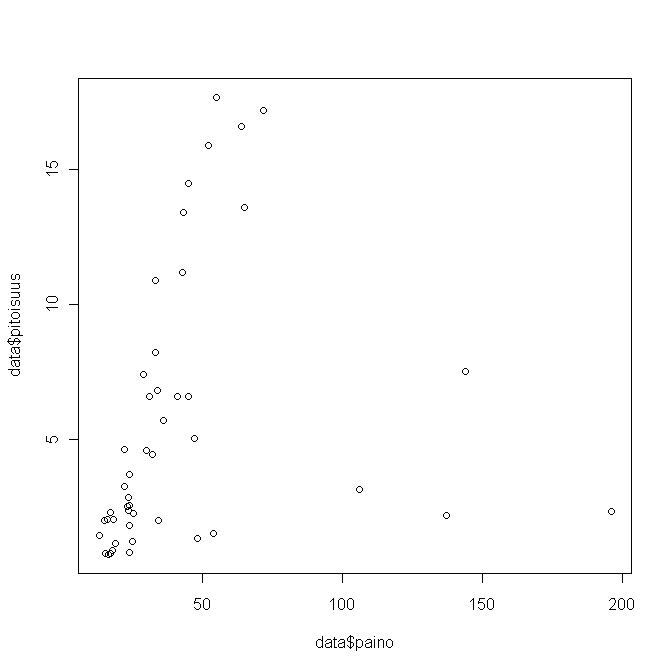
Kuva 2. Age against concentration in herring
Image:Ikä_vs_poitoisuus_silakka.jpg
Kuva 3.Weight against concentration in herring
Results of a linear regression model, where concentraition is explained with age and weight
Call: lm(formula = pitoisuus ~ ikä + paino, data = data)
Residuals: Min 1Q Median 3Q Max -7.9395 -1.3808 -0.1211 1.2573 6.4274
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.68568 0.78077 -2.159 0.0363 * ikä 1.66347 0.14978 11.106 2.39e-14 *** paino -0.03660 0.01205 -3.038 0.0040 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.575 on 44 degrees of freedom Multiple R-squared: 0.7495, Adjusted R-squared: 0.7381 F-statistic: 65.82 on 2 and 44 DF, p-value: 5.952e-14
Huomataan siis että ikä ja paino merkitseviä selittäjiä.
We notice that both age and weight are significant explanators.
Results of WinBUGS calculations
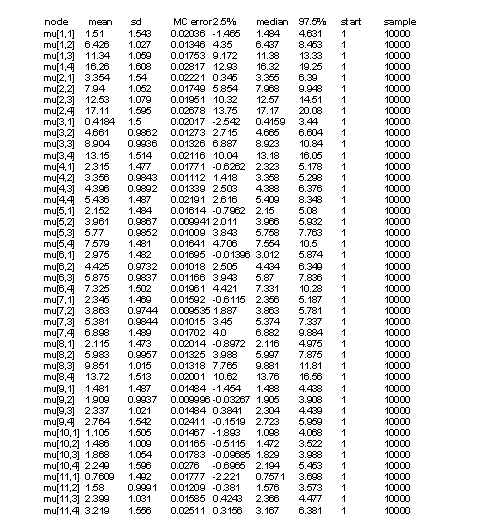
Tables 2 and 3 represent results of our model. In Y[1,2], the first parameter denotes to concentraion of on year old herring in location one (=1), and the second parameter denotes to age category (=2). Thus, the first parameter stands for location and the second parameter for age. Some values (confidence intervall 2.5%) are less than zero (which is not plausible as concentrations can not be negative), but we can control this by not allowing values below zero in our model. In table 3 there are ages divided into four categories (including three years each) and estimates for concentrations. Median values do not have values below zero but 2.5% CI has negative values. Estimates in table 2 are for missing values only. Medians seem to be quite good estimates but the confidence intervalls span very wide due to lack of data.
Table 2. List of results for herringdata with one year age intervals (WinBUGS). 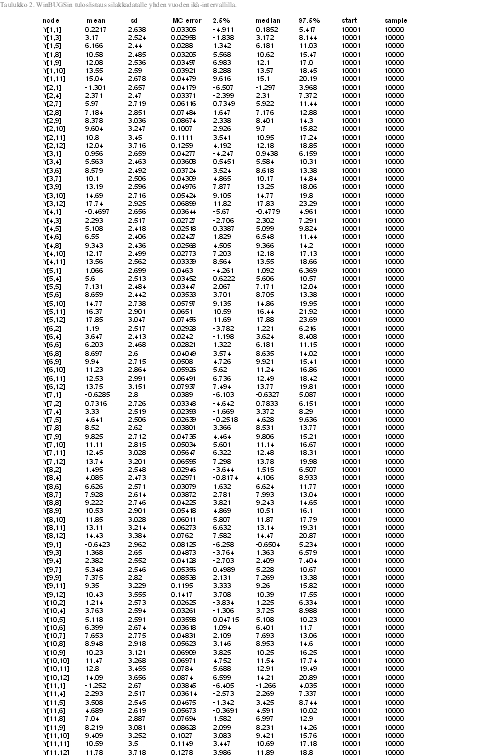
Table 3. List of results for dioxin concentration in herring with three year age intervall (Win BUGS)
See table 4 for Original data of herring
Syntaxes and iterations
Attached are the code of the model (model1, noodle_1 and data_1). There are age groups 1-4 and data_1 for each age categories, as well as inits (if we don't want to simulate them).
All codes open with WinBUGS program and are updated freely. Simulations are using model1 and data_1 and they are working with inits. Similar model can be found in examples (help menu) vol1 Rars. Setting a limit is done by adding syntax I(0,) to the end of distribution definition.
Running the model:
You need to open three windows. Under model find model specification, under inference find samples, and under model find update. With these, you can run the same calculations as we just did.
You can find the files from:
N:\Huippuyksikko\Tutkimus\R55_PMvsDioxin\MeHgvsOmega-3\mallit\Bayes\Aiemmat ajot ja pähkäilyt
Conculsions
We can compare the results with data and draw conclusions. The median estimates seem to have pretty ok values compared the the original data.
Rat example
This model can be found from WinBUGS help page. Our example is based directly to this model.
Rats: a normal hierarchical model
This example is taken from section 6 of Gelfand et al (1990), and concerns 30 young rats whose weights were measured weekly for five weeks. Part of the data is shown below, where Yij is the weight of the ith rat measured at age xj.
Weights Yij of rat i on day xj
| xj=8 | 15 | 22 | 29 | 36 | ||
| Rat 1 | 151 | 199 | 246 | 283 | 320 | |
| Rat 2 | 145 | 199 | 149 | 293 | 354 | |
| Rat 30 | 153 | 200 | 244 | 288 | 324 |
A plot of the 30 growth curves suggests some evidence of downward curvature.
The model is essentially a random effects linear growth curve
Yij ~ Normal(ai + bi(xj - xbar), Tc) ai ~ Normal(ac, Ta) bi ~ Normal(bc, Tb) where xbar = 22, and T represents the precision (1/variance) of a normal distribution. We note the absence of a parameter representing correlation between ai and bi unlike in Gelfand et al 1990. However, see the Birats example in Volume 2 which does explicitly model the covariance between ai and bi. For now, we standardise the xj's around their mean to reduce dependence between ai and bi in their likelihood: in fact for the full balanced data, complete independence is achieved. (Note that, in general, prior independence does not force the posterior distributions to be independent).
ac , ta?, bc , Tb?, Tc are given independent "noninformativepriors, with two alternatives considered for Ta and Tb: prior 1 is uniform on the scale of the standard deviations sa = 1/sqrt(Ta) and ab = 1/sqrt(Tb), and prior 2 is a gamma(0.001, 0.001) on the precisions Ta and Tb. Interest particularly focuses on the intercept at zero time (birth), denoted a0 = ac - vc xbar.
Graphical model for rats example (using prior 1):
BUGS language for rats example:
Note the use of a very flat but conjugate prior for the population effects: a locally uniform prior could also have been used.
Data list(x = c(8.0, 15.0, 22.0, 29.0, 36.0), xbar = 22, N = 30, T = 5, Y = structure( .Data = c(151, 199, 246, 283, 320, 145, 199, 249, 293, 354, 147, 214, 263, 312, 328, 155, 200, 237, 272, 297, 135, 188, 230, 280, 323, 159, 210, 252, 298, 331, 141, 189, 231, 275, 305, 159, 201, 248, 297, 338, 177, 236, 285, 350, 376, 134, 182, 220, 260, 296, 160, 208, 261, 313, 352, 143, 188, 220, 273, 314, 154, 200, 244, 289, 325, 171, 221, 270, 326, 358, 163, 216, 242, 281, 312, 160, 207, 248, 288, 324, 142, 187, 234, 280, 316, 156, 203, 243, 283, 317, 157, 212, 259, 307, 336, 152, 203, 246, 286, 321, 154, 205, 253, 298, 334, 139, 190, 225, 267, 302, 146, 191, 229, 272, 302, 157, 211, 250, 285, 323, 132, 185, 237, 286, 331, 160, 207, 257, 303, 345, 169, 216, 261, 295, 333, 157, 205, 248, 289, 316, 137, 180, 219, 258, 291, 153, 200, 244, 286, 324), .Dim = c(30,5)))
(Note: the response data (Y) for the rats example can also be found in the file ratsy.odc in rectangular format. The covariate data (X) can be found in S-Plus format in file ratsx.odc. To load data from each of these files, focus the window containing the open data file before clicking on "Data" from the "Model" menu.)
Inits1 list(alpha = c(250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250), beta = c(6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6),
alpha.c = 150, beta.c = 10, tau.c = 1, sigma.alpha = 1, sigma.beta = 1)
Inits2 list(alpha = c(250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250), beta = c(6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6), alpha.c = 150, beta.c = 10, tau.c = 1, tau.alpha = 1, tau.beta = 1)
Results
A 1000 update burn in followed by a further 10000 updates gave the parameter estimates:
node mean sd MC error 2.5% median 97.5% start sample alpha0 106.6 3.65 0.04151 99.43 106.5 113.9 1001 10000 beta.c 6.185 0.1102 0.001294 5.967 6.185 6.404 1001 10000 sigma 6.074 0.4673 0.007724 5.247 6.044 7.068 1001 10000
Using Prior 2 (not recommended) has negligible impact
These results may be compared with Figure 5 of Gelfand et al 1990 --- we note that the mean gradient of independent fitted straight lines is 6.19.
Gelfand et al 1990 also consider the problem of missing data, and delete the last observation of cases 6-10, the last two from 11-20, the last 3 from 21-25 and the last 4 from 26-30. The appropriate data file is obtained by simply replacing data values by NA (see below). The model specification is unchanged, since the distinction between observed and unobserved quantities is made in the data file and not the model specification.
click on one of the arrows to open the data for the missing value analysis
Gelfand et al 1990 focus on the parameter estimates and the predictions for the final 4 observations on rat 26. These predictions are obtained automatically in BUGS by monitoring the relevant Y[ ] nodes. The following estimates were obtained:
We note that our estimate 6.58 of bc is substantially greater than that shown in Figure 6 of Gelfand et al 1990. However, plotting the growth curves indicates some curvature with steeper gradients at the beginning: the mean of the estimated gradients of the reduced data is 6.66, compared to 6.19 for the full data. Hence we are inclined to believe our analysis. The observed weights for rat 26 were 207, 257, 303 and 345, compared to our predictions of 204, 250, 295 and 341.
Table 4. Original data for herring
| Age | Weight | Concentration |
| 2 | 15 | 1.96 |
| 4 | 23 | 2.49 |
| 6 | 31 | 6.58 |
| 7 | 43 | 13.4 |
| 11 | 71.7 | 17.2 |
| 2 | 17,6 | 0.876 |
| 3 | 25.2 | 2.22 |
| 3 | 34.1 | 1.99 |
| 5 | 54 | 1.5 |
| 6 | 137 | 2.18 |
| 2 | 18 | 2 |
| 2 | 24 | 2.52 |
| 6 | 33 | 8.23 |
| 9 | 52 | 15.9 |
| 11 | 64 | 16.6 |
| 2 | 16.3 | 0.704 |
| 4 | 23.6 | 2.84 |
| 7 | 34 | 6.79 |
| 9 | 45 | 14.5 |
| 12 | 65 | 13.6 |
| 2 | 17 | 2.29 |
| 3 | 24 | 3.67 |
| 7 | 33 | 10.9 |
| 8 | 42.9 | 11.2 |
| 9 | 55 | 17.7 |
| 1 | 15.3 | 0.733 |
| 3 | 23.5 | 2.35 |
| 5 | 30 | 4.59 |
| 7 | 41 | 6.59 |
| 3 | 15.8 | 2.02 |
| 6 | 22 | 4.6 |
| 7 | 29 | 7.4 |
| 7 | 47 | 5.03 |
| 6 | 144 | 7.52 |
| 1 | 19 | 1.13 |
| 3 | 25 | 1.186 |
| 5 | 36 | 5.7 |
| 2 | 13 | 1.42 |
| 5 | 22 | 3.25 |
| 6 | 32 | 4.44 |
| 8 | 34 | 6.58 |
| 10 | 106 | 3.13 |
| 1 | 17 | 0.768 |
| 3 | 24 | 1.79 |
| 2 | 24 | 0.782 |
| 3 | 48 | 1.29 |
| 7 | 196 | 2.31 |
Tutkittava asia Panulle:
Summa PBDE pitoisuus
Luokitus ensisijaisesti rasvaprosentin mukaan (vaihtoehtoisesti ikä, paino tai pituus). Jaetaan neljään lohkoon (esim. rasvaprosentti 0-2, 2-4, 4-6, >6)
Kokeile eri kategoriointa (rasvaprosentti, ikä, paino, pituus) mikä parhaiten selittää PBDE -pitoisuuden muuttumista.
Samaan tapaan kuin aiempi silakka-data. Priori-jakauma tulee kaikista PBDE-mittauksista ja rasvapidoisuuden täydentävä data tulee kustakin saman rasvapitoisuusluokan omaavista kaloista.
Data kirjasta Hallikainen et al. 2004. Sivut 17- 36. Kotimaisten järvi- ja merikalan dioksiinien, furaanien, dioksiinien kaltaisten PCB –yhdisteiden ja polybromattujen difenyylieettereiden pitoiuudet. EU-kalat. Elintarvikeviraston julkaisuja. Helsinki 2004.
See also
- SHELF package for R and MATCH online tool
- Hierarchical Bayesian model of Russian duma election 2011
- OpenBUGS model about election (does not work)
- rjags test (password required)
- rbugs test (password required) (rjags in CRAN)
- Benefit-risk assessment of Baltic herring
References
1) Gelman Andrew, Carlin John B., Stern Hal S., and Rubin Donald B. Bayesian data analysis – second edition. Chapman & Hall/CRC 2004.