Variable

<accesscontrol>members of projects,,Workshop2008,,beneris,,Erac,,Heimtsa,,Hiwate,,Intarese</accesscontrol> <section begin=glossary />

Variable is a description of a particular piece of reality. It can be a description of physical phenomena, or a description of value judgements. Also decisions included in an assessment are described as variables. Variables are continuously existing descriptions of reality, which develop in time as knowledge about them increases. Variables are therefore not tied into any single assessment, but instead can be included in other assessments. A variable is the basic building block of describing reality.<section end=glossary />

The research question about the structure of a variable

What is a structure of a variable such that it

• is able to systematically handle all kinds of information about the particular piece of reality that the variable is describing,
• is able to systematically describe causal relationships between variables,
• enables both quantitative and qualitative descriptions,
• is suitable for any kinds of variables, especially physical phenomena, decisions, and value judgements,
• inherits its main structure from universal objects,
• complies with the PSSP ontology,
• can be operationalised in a computational model system,
• results in variables that are independent of the assessment(s) it belongs to;
• results in variables that pass the clairvoyant test.

Attribute	Sub-attribute	Comments specfic to the variable attributes
Name
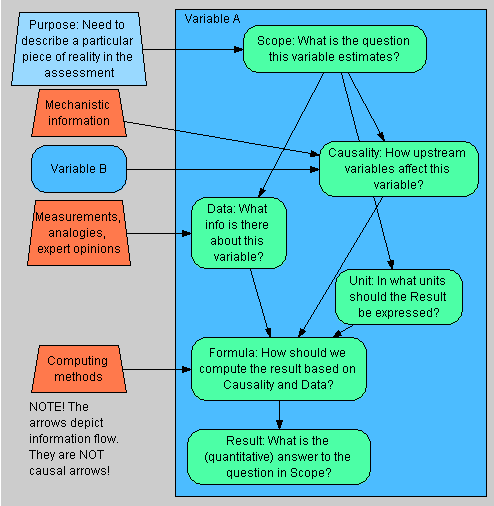
Scope		This includes a verbal definition of the spatial, temporal, and other limits (system boundaries) of the variable. The scope is defined according to the use purpose of the assessment(s) that the variable belongs to.
Definition	Causality	Causality tells what we know about how upstream variables (i.e. causal parents) affect the variable. Causality lists the parents and expresses their functional relationships (the variable as a function of its parents) or probabilistic relationships (conditional probability of the variable given its parents). The expression of causality is independent of the data about the magnitude of the result of the variable.
	Data	Data tells what we know about the magnitude of the result of the variable. Data describes any non-causal information about the particular part of reality that is being described, such as direct measurements, measured data about an analogous situation (this requires some kind of error model), or expert judgment.
	Unit	Unit describes, in what measurement units the result is presented. The units of interconnected variables need to be coherent with each other given the functions describing causal relations. The units of variables can be used to check the coherence of the causal network description. This is a so called unit test.
	Formula	Formula D↷ is an operationalisation of how to calculate or derive the result based on Causality, Data, and Unit, making a synthesis of the three. Formula uses algebra, computer code, or other explicit methods if possible.
Result		A result is an estimate about the particular part of reality that is being described. It is preferably a probability distribution (which can in a special case be a single number), but a result can also be non-numerical such as "very good".

Specific issues related to variable attributes

In a general form, the formula can be described as

result = formula(causal parameters, data parameters, unit), 

where formula is the function (expressed as computer code for a specified software) for calculating the result using the causal parameters (information from causally upstream variables) and the data parameters (information from observed data) as input.

It should be noted that the result is the distribution itself, although it can be expressed as some kind of description of the distribution, such as mean and standard deviation. The result should be described in such a detailed way that the full distribution can be reproduced from the information presented under this attribute. A technically straightforward way to do this is to provide a large random sample from the distribution.

The result may be a different number for different locations, such as geographical positions, population subgroups, or other determinants. Then, the result is described as

  R|x1,x2,... 

where R is the result and x₁ and x₂ are defining the locations. A dimension means a property along which there are multiple locations and the result of the variable may have different values when the location changes. In this case, x₁ and x₂ are dimensions, and particular values of x₁ and x₂ are locations. A variable can have zero, one, or more dimensions. Even if a dimension is continuous, it is usually operationalised in practice as a list of discrete locations. Such a list is called an index, and each location is called a row of the index.

Uncertainty about the true value of the variable is one dimension. The index of the uncertainty dimension is called the Sample index, and it contains a list of integers 1,2,3... . Uncertainty is operationalised as a sequence of random samples from the probability distribution of the result. The i^th random sample is located in the i^th row of the Sample index. In other words random samples are used to describe the distribution of the results performing Monte Carlo analysis. D↷

Technical issues in Mediawiki

----#(number):: . This should be moved. Where? --Jouni 20:00, 9 June 2008 (EEST) (type: truth; paradigms: science: comment)

• Each variable is a page in the Variable namespace. The name of the variable is also the name of the page. However, draft variables may be parts of other pages.
• All attributes except name are second-level (==) sub-titles on the page.
• Description of the attribute content is added at the end of that content; discussions on the content are added to the Talk page, each discussion under an own descriptive title.
• References to external sources are added to the text with the <ref>Reference information</ref> tag. The references are located in the end of the page under subtitle References. However, reference is not an attribute of the variable despite it is technically similar.
• In the formula, computer code for a specific software may be used. The following are in use.
  • Analytica_id: Identifier of the respective node in an Analytica model. <anacode>Place your Analytica code here. Use a space in front of each line.</anacode>
  • <rcode>Place you R code here. Use a space in front of each line.<rcode>

Event-substance

----#(number):: . This paragraph should be deleted or removed. Where? --Jouni 00:40, 8 June 2008 (EEST) (type: truth; paradigms: science: comment)

Variables are objects of event-medium composite -type. They thus describe both the events that occur within the scope of the variable and the medium where these particular events take place. In practice, the events can only be observed through the changes in the state of the medium, and it is therefore reasonable to describe the events and particular media as such composites rather than as separately.

In open assessment, all the variables included in an assessment must be causally related, directly or indirectly, to the endpoints of the assessment, and the causal relations must be defined. The event-media structure is the carrier of the cause-effect relations between the variables. An event occuring in a medium causes a change in state of that medium leading to another event to occur changing the state of that medium, causing yet another event to occur and so on. In addition to variables, also classes as generalizations of properties possessed by variables can be causally related to each other.

See also

• Open assessment
• A previous version of this page contains much of the discussion from the Intarese deliverables D17 and D18, which has been edited with a hard hand.