Piloting: Defining and describing uncertainties

Defining and describing uncertainties

Assessing complex policy problems such as those that are the target of integrated environmental health impact assessments inevitable involves major uncertainties. Doing an assessment without considering these uncertainties is a pointless task; likewise, presenting the results of an assessment without giving information about the uncertainties involved makes the results more-or-less meaningless. The uncertainties likely to be encountered therefore need to be considered at the feasibility testing stage, in order to ensur that an assessment is worthwhile, that it is better to undertake an assessment now rather than wait for better information (so that the uncertainties can be reduced), and - if an assessment is to proceed - to work out how to deal with the uncertainties involved.

The dimensions of uncertainty

Uncertainties arise at every step in an assessment: from the initial formulation of the question to be addressed to the ultimate reporting and interpretation of the findings. They also take many different forms, and are not always immediately obvious. It is therefore helpful to apply a clear and consistent framework for identifying and classifying uncertainties, in order to ensure that key sources of uncertainty are not missed and that users can understand how they arise and what their implications might be. In particular, it is useful to distinguish between two essential properties of uncertainty:

location - where within the analytical process (and embedded causal) chain it arises level - its magnitude or degree of importance

Describing uncertainties

It is also important to describe and, where possible, quantify the uncertainties that arise during the assessment. The best way of doing this is likely to vary, depending on the issue and the assessment methds being used. In some cases, rigorous statistical methods can be used, epecially where the main uncertainties relate to sampling or measurement error. In other cases, more qualitative methods are more appropriate. To describe all the main sources of uncertainty in a large and complex assessment may need some combination of these techniques. The problem of this is that it can then be difficult to compare the degree of uncertainty inherent in different parts of the process, or to derive an overall measure for the assessment as a whole. In selecting a method for describing uncertainty, therefore, we need to consider not only its scientific rigour, but also its appicability to the sorts of data and types of uncertainty involved. In the end, it may be more informative to use a simple yet consistent method, which includes all the main uncertainties in the assessment, rather than a more sophisticated one which only considers some of them.

Framework for uncertainty classification

Uncertainty can be defined as any departure from the unachievable ideal of complete deterministic knowledge of the system.

From the point of view of health impact assessment, uncertainty is best thought of as comprising two distinct properties: location and level.

Location of uncertainty refers to where uncertainty manifests itself within the system model that is used in the assessment. The way location is described and classified depends both on the issue under investigation and the analytical approach that is used. In the case of integrated environmental health impact assessment, however, two related dimensions need to be considered:

• the analytical model - where uncertainties arise within the process from initial poblem definition to final comparison and ranking of the impacts;

• the conceptual model - where uncertainties develop within the casual chain between source and impact.

The former is described mainly in terms of what is referred to as inputs, parameters and outputs; the latter is characterised mainly by what is known as context and model structure uncertainty (i.e. what is included in the assessment and how these components are defined).

In many cases, it may be appropriate to separate these, since they relate to different, and largely independent, aspects of the assessment, which pose different challenges for assessment design. Uncertainties in the analytical model, for example, are best dealt with by improvements in the data and methods of analytical methods used for assessment. Uncertainties in the conceptual model (e.g. in the choice of what to include or exclude from the assessment, or how the specific causal relationships are defined) imply the need to reconsider and revise the way in which the issue has been defined and framed.

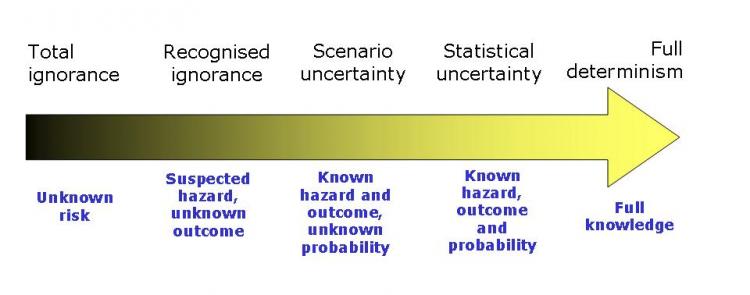
Level of uncertainty refers to the degree to which the object of study is uncertain, from the point of view of the decision maker. The figure below provides a graphic illustration of levels of uncertainty, in which five different states can be recognised:

1. Determinism - i.e. complete knowledge, with no uncertainty

2. Statistical uncertainty - i.e. where likely consequences are known and their probabilities can be quantified

3. Scenario uncertainty - i.e. where the likely consequences are known, but their probabilities cannot be quantified

4. Recognised uncertainty - i.e. where even the likely consequences are not clear

5. Total ignorance - i.e. where nothing is known on which to make judgements about what may happen.

Location of uncertainty

The description of the locations of uncertainty will vary according to the assessment method (model) that is in use. Nonetheless, it is possible to identify certain categories of locations that apply to most models.

• Context refers to the choice of the boundaries of the system to be modeled. This location is of great importance, as the choice of the boundaries of the system determines what part of the real world is considered inside the system (and therefore the model), and what part of the real world is left out. The choice of the system boundaries is often referred to as the 'problem framing', 'problem definition' or “issue framing”. Different stakeholders have different perceptions of what constitutes a risk, which risks should be assessed, and how much risk is acceptable, so contextual uncertainties may be a cause for considerable debate during (and after) an assessment.

• Model structure refers to the variables, parameters and relationships that are used to describe (model) a given phenomenon. Model structure uncertainty is thus uncertainty about the form of the model that describes the phenomena included within the boundaries of the system. Here one could think of the shape of dose-response functions, or the additivity vs. the multiplicativity of risk factors. In situations where the system being studied involves the interaction of several complex phenomena, different groups of analysts may have different interpretations of what the dominant relationships in the system are, and which variables and parameters characterise these relationships. Uncertainty about the structure of the system implies that any one of many model formulations might be a plausible, although partial, representation of the system. Thus, analysts with competing interpretations of the system may be equally right, or equally wrong.

• Inputs refers to the data describing the system. Uncertainty about system data can be generated by insufficient or poor quality data. Measurements can never exactly represent the 'true' value of the property being measured. Uncertainty in data can be due to sampling error, measurement inaccuracies or imprecision, reporting (e.g. transcribing) errors, statistical (e.g. rounding or averaging errors), conflicting data or simply lack of measurements.

• Parameters comprise the specific, quantifiable variables used to describe the system being modelled. Three main types of parameter can be specified:
  • Exact parameters (e.g. π and e);
  • Fixed parameters, (e.g. the gravitational constant g); and
  • A priori chosen or calibrated parameters.

The uncertainty on exact and fixed parameters can generally be considered as negligible within the analysis. However, extrapolation of parameter values from a priori experience does lead to parameter uncertainty, as past circumstances are rarely identical to current and future ones. Calibrated parameters are also subject to uncertainty because calibration has to be done using historical data series, and sufficient (i.e. representative) calibration data may not be available, while errors may be present in the data that are available.

• Model outcome (result) is the uncertainty caused by the accumulation of uncertainties from all of the above locations (context, model, inputs, and parameters). These uncertainties are propagated throughout the model and are reflected in the resulting estimates of the outcomes of interest (model result). It is sometimes called prediction error, since it is the discrepancy between the true value of an outcome and that predicted by the model.

Example: Location of uncertainty

Consider a map of the world that was drawn by a European cartographer in the 15th century.
Such a map would probably contain a fairly accurate description of the geography of Europe.
Because the trade of spices and other goods between Europe and Asia was well established at that time,
one might expect that those portions of the map depicting China, India, central Asia and the middle-east were also fairly
accurate. However, as Columbus only ventured to America in 1492, the portions of the map depicting the American continent
would likely be quite inaccurate (if they existed at all). Thus, it would be possible to point to the American continent
as a 'location' in the model that is subject to large uncertainty. In this case, the model in question is a map of the world,
and all locations are geographic components of the map.