Impact calculation tool

This page is a knowledge crystal of subtype method. The page identifier is Op_en2909
Moderator:Virpi Kollanus (see all)
Citation of this page: Virpi Kollanus, Anne Knol, Olli Leino: Impact calculation tool. Opasnet 2010. [1]. Accessed 27 Nov 2024.
Upload data {{#opasnet_base_link:Op_en2909}}

The Impact calculation Tool -model can be downloaded from this link:

File:Impact Calculation Tool.ana

Short overview of the impact calculation tool

Impact Calculation Tool (ICT) is a modelling tool for quantification of health impacts from environmental exposures. It applies dynamic life table modelling for calculating target population specific mortality and morbidity impacts. The model has been developed in the context of international projects working on environmental health impact assessment (Intarese, Heimtsa) and the Finnish Academy project CLAIH, and is a collaboration between the National Institute of Health and Welfare (THL, Finland), the National Institute for Public Health and the Environment (RIVM, the Netherlands), and Netherlands Environmental Assessment Agency (PBL, the Netherlands).

ICT has been developed to provide answers to questions such as:

What is the burden of disease (BoD) attributable to a given environmental exposure (i.e. environmental burden of disease, EBD) in a given target population?

How much does the burden of disease change if the exposure changes?

ICT allows analysis of health impacts from one environmental exposure in one given population at a time. The follow-up period (time period for which impacts are determined), specific mortality and morbidity impacts analysed, and the target population can be defined according to the needs of the assessment at hand. In one model run, impacts are modelled for a reference, business-as-usual (BAU), and one alternative exposure scenario. Both time discounting and age-weighting can be applied.

Health impacts can be quantified using different approaches depending on the type of input data available for the analysis:

Modelling approach 1: Life table method

User defines exposure or health outcome scenarios and provides exposure-response relationships, background mortality and, if needed, morbidity data for the population and health outcomes of interest. The model then calculates the mortality or morbidity risks attributable to the exposure in different scenarios, makes population projections for the future using dynamic lifetables, and based on these derives the different health impact indicators.

Modelling approach 2: Calculation of EBD from BoD

User defines exposure scenarios and provides exposure-response relationships and BoD data (e.g. from WHO) for the health outcomes of interest. The model then calculates the fraction of BoD caused by the risk factor in the business-as-usual (BAU) scenario. Environmental burden of disease in a theoretical Alternative exposure can also be calculated. In this approach, the assessment time frame is limited to the time frame of the total BoD data provided.

Input data requirements vary between different modelling approaches, but may include

• Age-specific population data
• Age-specific baseline mortality incidence and morbidity incidence/prevalence data
• Birth rate
• Exposure levels
  • Business-as-usual (BAU) scenario
  • Alternative scenario
  • Reference scenario (no exposure or natural background exposure)
• Exposure-response functions for the health endpoints of interest (relative risk or absolute risk)
• Severity weights and durations for the morbidity endpoints

The model itself does not contain a database or default values for the required input data, but functions more like a calculation shell. All key input data has to be provided by the user, and needs to be preprocessed to be in the correct form.

Model outputs vary between the different modelling approaches, but include

• Loss of disability adjusted life years (DALY)
  • Years lost due to mortality (YLL)
  • Years lost due to disability (YLD)
• Age-specific loss of life-expectancy for target population
• Average loss of life-expectancy for a birth cohort
• Number of attributable deaths
• Number of attributable morbidity cases

ICT runs in Analytica software, which enables probabilistic modelling using Monte Carlo simulation and, therefore, advanced uncertainty analysis. Probabilistic modelling of uncertainty requires the key model inputs to be defined in terms of probability distributions. As a result, the uncertainty in the model outputs can be viewed with basic statistical descriptors, probability bands, probability density functions, and cumulative probability density functions.

Full use of the Analytica programme requires a software licence. However, ICT can also be run with a free Analytica player, which can be downloaded from lumina.com. The player allows the user to view to the model contents and calculation specifics, to input data for key parameters, and to calculate results and run probabilistic uncertainty analysis. ICT contains a simple user interface, which enables these functions without advanced knowledge of Analytica or the model technicalities. Analytica also has several built-in functions for conducting sensitivity analyses for both deterministic and probabilistic analyses. However, these functions are not incorporated into the user interface and their use requires advanced model editing.

Background information

Environmental health impact assessment

Environmental problems such as air pollution or radon can affect human health. Several scientific methods have been developed in order to estimate the extent of such environmental health impacts, or the potential impact of policy and plans on these impacts. These methods include health impact assessment, integrated assessment and risk assessment. When such assessments deal with complex environmental health problems, such as transport or climate change, the effects of different environmental risks often need to be compared. Traditionally, numbers of attributable deaths and disease cases were reported. Such numbers can supply useful information, but cannot always be used to compare dissimilar health effects. For example, effects from air pollution range from aggravation of asthma to premature mortality, while noise exposure is associated with annoyance, sleep disturbance and effects on cognition. Because of the divergence in magnitude, duration and severity of these health effects, summary health measures have been developed. Such measures convert all health effects to a comparable unit, and can thus be very useful for the interpretation and comparison of different (environmental) health problems. This is especially useful for evaluating and comparing different policy options and assessing cost effectiveness of mitigating measures or prevention. Summary health measures in environmental health decision-making include for example Years of Life Lost (YLL), disease burden estimates such as Disability Adjusted Life Years (DALYs) or monetary valuation.

Indicators that can be calculated using ICT

As will be described in detail below, the Impact Calculation tool is able to calculate a variety of (summary) health measures. Which indicator is feasible to calculate depends on the data that are available. Which indicator is most suitable to calculate, depends on the type of assessment carried out, the underlying assumptions and the needs and wishes of the assessor and other stakeholders.

Number of attributable deaths

The number of attributable deaths provides an estimate of the number of people that die due to a specific environmental exposure in a specific time period. Even though this indicator is often used and considered by some to be of high communicative value, its calculation and interpretation are not as straightforward as it may seem at first sight. Issues that play a role when calculating attributable deaths include:

• what is an ‘attributable’ death, especially in case of multi-causality (e.g. when someone’s death is caused by a combination of factors, such as exposure to air pollution, bad dietary habits and insufficient physical activity)
• what is an ‘extra’ death: everybody will die at some point
• what is a ‘premature’ death: this would imply that we know what a ‘mature death’ is.

Also, estimates of numbers of attributable deaths are only valid for the year (or other period) for which they were calculated.

In addition, and in relation to the latter point: numbers of deaths do not provide any information about the age of the people that die. Most people will agree that it is worse when a 50-year-old dies due to radon-induced lung cancer than when a 85 years old during due to a smog episode. Such information is included in estimates of lost life expectancy or years of life lost (see later). The indicators also avoid some of the issues mentioned above.

Nonetheless, estimates of attributable deaths can be useful in some instances, but only if:

• calculated for a specific time period
• calculated for mono-causal effects
• interpreted correctly

For more information about limitations and interpretation of attributable deaths, see: [2]

Number of attributable morbidity cases

Similar to the number of attributable deaths, the number of attributable morbidity cases provides an estimate of the amount of people that have a certain disease due to exposure to a specific environmental pollutant. Not all the limitations that apply to the use of attributable deaths also hold for attributable morbidity cases. Age of the persons with the disease or population dynamics over time are less relevant in case of morbidity. However, also here, in case of multi-causality it is especially important to correctly interpret the results.

A limitation of this indicator is the fact that the severity of the disease is not expressed and therefore it is not possible to make comparisons between environmental factors that cause different types of diseases. Nonetheless, just as numbers of attributable deaths, numbers of attributable disease cases may be attractive for their communicative value: they are easy to understand at first sight.

Age-specific loss of life-expectancy for target population

This indicator looks at the total number of people of a certain age in the target population at a certain time, and provides the estimated average (future) loss of life expectancy (due to mortality related to environmental exposures) per age group, compared to a reference exposure level. This indicator can be particularly relevant to present impacts that affect certain age categories more than others. It avoids most of the limitations mentioned above for attributable deaths. One limitation that obviously remains is that it only provides information about mortality; morbidity effects are not included.

Average loss of life-expectancy for a birth cohort

When the model is used to calculate the estimated average loss of life-expectancy for a birth cohort, it looks at one group of people born in a specific year (the cohort) and follows this group over the years until every group member has died. The average life expectancy from this group is then compared to the life expectancy the group would have under the reference exposure scenario. The difference between these two estimates is the average loss of life-expectancy for the birth cohort.

Years lost due to mortality (YLL)

Using dynamic life tables, the model can calculate how many years of life are lost due to mortality related to the exposure in the exposed population. This estimate does not include morbidity effects. It does not give the number of people that are expected to die, but the total number of life years lost by the whole group. Therefore, it is a more valid indicator to express mortality related to chronic/ multi-causal effects than numbers of deaths (see above). The sum of YLL and YLD gives DALYs.

Years lost due to disability (YLD)

The years of life lost due to disability is the total number of years lived by a population in a certain disease state, weighted for the severity of the disease. For this severity of different disease states, so-called severity weights (or disability weigts) have been developed. These weights give an indication of the reduction in capacity due to the specific disease. A weight factor, varying from 0 (healthy) to 1 (death), is determined by experts (clinicians, researchers, etc). An overview of severity weights that have been collected in various studies can be found in http://www.health.vic.gov.au/healthstatus/downloads/bod_2001d.pdf (appendix 1 of that pdf). YLD is seldom used as a separate indicator. Moreover, it is used is input for DALY calculations.

Loss of disability adjusted life years (DALY)

DALYs are the sum of YLL and YLD (see above). As such, DALYs combine information on quality and quantity of life. They give an indication of the (potential) number of healthy life years lost due to mortality or morbidity.

In a simplified version, the formula of a DALY is as follows:

Number of people with environment-related morbidity or mortality * Severity factor for a condition (0 = healthy, 1 = death) * Duration of condition

DALY calculations can also include discounting factors. In discounting, future years of healthy life lived are valued less than present years (discounting normally 3%), or years lived by people in a certain age group (productive ages) are valued more than years lived by the very old and young. In the ICT model, discounting is optional.

Age-weighing is also optional. Age-weighing implies valuing years lived at a certain age more than years lived at other ages (normally, people of around 25 years old are valued more than babies or the very old).

Both discounting and age-weighing can raise ethical questions. DALYs capture number of people, duration and severity of conditions in one number, thereby greatly simplifying reality. This simplification can be very useful to make different health states or environmental disease burdens comparable, but it may also lead to significant uncertainty in the output.

Uncertainty can relate to for example:

• Definitions (what is ‘health’? what is ‘environment’?)
• Assumptions in the model (for example: causality)
• Data (concentrations / emissions, exposed population, dose effect relationships)

(see for more information about uncertainties in DALYs also http://www.ehjournal.net/content/8/1/21/)

DALYs should therefore always be interpreted taking their context and input data into account. They can only be used to give an indication of the potential order of magnitude of different (environmental) health problems, and can not be presented as absolute or completely representative numbers.

Life table modelling

The advantage of dynamic life table modelling in health impact assessment is that it enables to predict impacts in a real life population over time as the population structure and risk level changes. Full use of a life table model also takes into account that changing the risk of a certain cause of death at a given point in time will affect the population available to die from any cause of death at later time points. Thus, it gives the net change in the life years saved or lost over time and prevents over-estimation of the overall mortality impact when evaluating effects from multiple mortality endpoints for a single exposure or combined mortality effects from multiple exposures.

Life table modelling provides most benefits in terms of estimating the net total impacts in a real life population when used in a direct way, i.e. comparing the life years lived in different scenarios calculated directly from the population projections. However, the indirect use, i.e. when life table modelling is used to determine age-conditional life expectancy in a real life population, which can be further multiplied with attributable deaths to derive YLL, can be more preferable in some situations. This is, for example, in cases where impacts are modelled for a short follow-up period (one or few years), but the aim is to estimate total loss of life years due to the attributable deaths. A simplified solution would be to use age-conditional life expectancy data for the current population. However, if the aim is to model impacts due to an existing risk factor, this approximation would lead to underestimation of YLL because it ignores that in the (theoretical) absence of the risk life expectancy would, in fact, be a fraction higher. In many cases this difference would be negligible, but could in some cases be of importance. This source of bias is avoided when applying life table modelling in the impact assessment, because the model also predicts the impact of the risk factor to the current life-expectancy in the target population.

Model description: Life table method

Summary

Mortality impacts are modelled using the dynamic life table method. First, total mortality risk in different exposure scenarios is determined based on input data on population, mortality, exposure levels and exposure-response functions. Based on the modelled total mortality risk in different scenarios and population input data, the future population structure is then projected for each scenario using life table methodology. These population projections are used in determining the life years lived by different age cohorts, and the age-conditional life expectancies in the different scenarios are derived from these. YLL (years of life lost due to mortality) can subsequently be calculated directly as the difference in the total life years lived in different scenarios, or indirectly based on the age-specific attributable (cause-specific) deaths in a given scenario and age-specific life expectancy in the Reference (i.e. zero or background exposure level) scenario.

Morbidity impacts are modelled by first deriving the morbidity risk attributable to the exposure in different scenarios based on input data on population, morbidity, exposure levels and exposure-response functions. Number of attributable morbidity cases is then calculated using the attributable morbidity risk and the modelled population projections for each scenario, and YLD (years of life lost due to disease) subsequently based on the attributable cases, severity weight and duration.

The following chapters provides a general overview of the modeling principles applied in the Impact calculation tool. A detailed description for the code in the different calculation nodes in the model can be found here: Impact Calculation Tool code description.

Mortality risk

When starting point for the assessment is 'Exposure scenarios':

For those mortality endpoints for which the exposure-response function applied is a relative risk (RR) function:

1) Calculation of a baseline mortality risk, i.e. mortality risk in the (theoretical) absence of the exposure of interest:

BMR = Mortality / Population * (1 - AFMortality data)

• BMR = Mortality risk in the absence of the exposure of interest
• Mortality = Annual mortality based on the mortality input data
• Population = Population based on the population input data
• AF_{mortality data} = Fraction of mortality cases attributable to the exposure/risk factor of interest in the mortality input data

AFMortality data = (RR’BAU - 1) / RR’BAU

• RR’_BAU = Relative risk adjusted to the exposure level in BAU scenario (the exposure level in the first 5-year time step if exposure is defined to vary through follow-up period)

RR’BAU = Exp(ln(RR) / Unit * ExposureBAU)

• RR = Relative risk per unit of exposure
• Unit = Exposure unit
• Exposure_BAU = Exposure level in BAU scenario (the exposure level in the first 5-year time step if exposure is defined to vary through follow-up period)

Average adjusted relative risk in the whole population is calculated based on the fraction of exposed population. The non-exposed population is assumed to expose to the reference scenario level (i.e. zero or natural background exposure).

2) Calculation of mortality risk in different exposure scenarios (and in different 5-year time steps if exposure is defined to vary through follow-up period):

MR = BMR * RR’

• MR = Mortality risk in a given exposure scenario (and in a given 5-year time step if exposure is defined to vary through follow-up period)
• RR’ = Relative risk adjusted to the exposure level in a given scenario (and in a given 5-year time step if exposure is defined to vary through follow-up period)

RR’ = Exp(ln(RR) / Unit * Exposure)

• RR = Relative risk exposure-response function
• Unit = Exposure unit to which the RR relates to
• Exposure = Exposure level in different scenarios (and in different 5-year time steps if exposure is defined to vary through follow-up period)

For those mortality endpoints for which the exposure-response function applied is an absolute risk (AR) function:'

Calculation of the difference in mortality risk in different scenarios compared to the risk level in level in BAU scenario (the risk level in the first 5-year time step if exposure is defined to vary through follow-up period):

∆risk = AR / Unit * ∆exposure * Pop frac

• AR = absolute risk per unit of exposure
• Unit = Exposure unit
• ∆exposure = Difference between the exposure in BAU scenario (exposure level in the first 5-year time step if exposure is defined to vary through follow-up period) and the exposure in a given scenario
• Pop frac = Fraction of exposed population

This change is then then summed up to the mortality risk calculated based on the population and mortality input data.

When starting point for the assessment is 'Health outcome scenarios':

Mortality risk in BAU and Alternative scenarios:

MRBAU/Alternative = Mortality / Population + Mortality / Population *  AFMortality data * Mortality change / 100

• MR_{BAU/Alternative} = Mortality risk in Business-as-usual (BAU) / Alternative scenario
• Mortality = Annual mortality based on the mortality input data
• Population = Population based on the population input data
• AF_{Mortality data} = Fraction of mortality cases attributable to the exposure/risk factor of interest in the mortality input data
• Mortality change = Percentage change in attributable mortality risk in BAU / Alternative scenario

Mortality risk in Reference scenario:

MRReference = Mortality / Population * (1 - AFMortality data)

• MR_Reference = Mortality risk in Reference scenario
• Mortality = Annual mortality based on the mortality input data
• Population = Population based on the population input data
• AF_{Mortality data} = Fraction of mortality cases attributable to the exposure/risk factor of interest in the mortality input data

Population projection

Population structure is projected in 5-year age categories and 5-year time steps for a 100 year period beginning from the assessment start year. If the assessment follow-up period is shorter than 100 years, the mortality risk for the rest of the 100-year period is assumed to stay on the level it is in the last follow-up time step.

The modelling steps are:

1) Population age structure in the beginning of the assessment is defined by the population input data.

2) The annual survival rate for a given age category in a given 5-year time step is calculated as follows:

SR = 1 – MR

• SR = Annual survival rate in a given age category in a given 5-year time step
• MR = Annual total mortality risk in a given age category in a given 5-year time step

3) Survival rate from a given age category (x) to the next age category (x+1) during a 5-year time step is then calculated as follows:

SRtimestep = SRagecat(x)5 + (SRagecat(x)4 * SRagecat(x+1)) + (SRagecat(x)3 * SRagecat(x+1)2) + (SRagecat(x)2 * SRagecat(x+1)3) + (SRagecat(x) * SRagecat(x+1)4)

• SR_timestep = Survival rate from an age category (x) to the next age category (x+1) during a 5-year time step
• SR_agecat(x) = Annual survival rate in an age category (x)
• SR_agecat(x+1) = Annual survival rate in the next age category (x+1)

4) Number of population in a given age category in the beginning of a given 5-year time step is then calculated as follows:

Populationagecat(x),timestep(y) = Populationagecat(x-1),timestep(y-1) * SRtimestep,agecat(x-1)

• Population_{agecat(x),timestep(x)} = Number of population in a given age category (x) in the beginning of a given five-year time step (y)
• Population_{agecat(x-1),timestep(y-1)} = Number of population in a the previous age category (x-1) in the beginning of the previous five-year time step (y-1)
• SR_{timestep,agecat(x-1)} = Survival rate from the previous age category (x-1) to the given age category (x) during a 5-year time step

5) Average number of population in a given age-category in a given 5-year time step is then calculated as follows:

Average populationagecat(x),timestep(y) = (Populationagecat(x),timestep(y) + Populationagecat(x),timestep(y+1)) / 2

• Average population_{agecat(x),timestep(y)} = Average number of population in a given age-category (x) during a given five-year time step (y)
• Population_{agecat(x),timestep(y)} = Number of population in a given age-category (x) in the beginning of a given five-year time step (y)
• Population_{agecat(x),timestep(y+1)} = Number of population in the given age-category (x) in the beginning of the next five-year time step (y+1)

Life years lived

Life years lived in a given age-category in a given 5-year times step is calculated as follows:

Life yearsagecat(x),timestep(y) = (Populationagecat(x),timestep(y) * SRagecat(x),timestep(y) * 5 + Deathsagecat(x),timestep(y) * 2.5) * Age weightagecat(x) * PV life yeartimestep(y)

• Population_{agecat(x),timestep(y)} = Number of population in a given age category (x) in the beginning of a given 5-year time step (y)
• SR_{agecat(x),timestep(y)} = Survival rate from a given age category (x) to the next age category (x+1) in a given 5-year time step (y)
• 5 = Years lived by each surviving individual during a 5-year time step
• Deaths_{agecat(x),timestep(y)} = Number of deaths in a given age category (x) in a given 5-year time step (y)
• 2.5 = An average number of years lived by each individual who dies during a 5-year time step
• Age weight_agecat(x) = Age weight for a given age-category (x)
• PV Life year_timestep(y) = Present value of a life year lived in a given 5-year time step (y). Present time is the start year of the assessment.

Age-adjusted life expectancy

Life expectancyage cat(x) = (Life yearsage cat(x),timestep(1) + Life yearsage cat(x+1),timestep(2) + Life yearsage cat(x+2),timestep(3) + ... + Life yearsage cat(20),timestep(20)) / Populationage cat(x),timestep(1)

• Life years_{age cat(x...20),timestep(1...20)} = Life years lived by a given population age category cohort in a given 5-year time step from the beginning of the assessment to the end of a 100 year period. Age cat x = any age category between 1 (0-4 years old) and 20 (95-99 years old).
• Population_{age cat(x),timestep(1)} = Number of population in a given age cohort in the start of the assessment (determined based on the population input data).

Attributable deaths

Deaths attributable to the exposure of interest in BAU/Alternative scenarios are calculated for different age-categories and 5-year follow-up time as follows:

Attributable deaths = (MR - MRreference) * Average population

• MR = Annual mortality risk in a given age-category and 5-year time step in BAU/Alternative scenario
• MR_{reference,age} = Annual mortality risk in a given age-category in the Reference scenario (i.e. zero or natural background exposure level)
• Average population = Average number of population in a given age-category and 5-year time step in BAU/Alternative scenario

Attributable morbidity cases

When starting point for the assessment is 'Exposure scenarios':

For morbidity endpoints for which the exposure-response function applied is a relative risk (RR) function:

1) Calculation of a baseline morbidity risk, i.e. a (theoretical) morbidity risk in the absence of the exposure of interest:

BDR =  Morbidity / Population * (1 - AFMorbidity data)

• BDR = Morbidity risk in the absence of the risk factor
• Morbidity = Annual morbidity based on the morbidity input data
• Population = Population based on the population input data
• AF_{Morbidity data} = Fraction of morbidity cases attributable to the exposure/risk factor of interest in the morbidity input data

AFmorbidity data = (RR’BAU-1) / RR’BAU

• RR’_BAU = Relative risk adjusted to the exposure level in BAU scenario (the exposure level in the first 5-year time step if exposure is defined to vary through follow-up period).

RR’BAU = Exp(ln(RR) / Unit * ExposureBAU)

• RR = Relative risk per unit of exposure
• Unit = Exposure unit
• Exposure_BAU = Exposure level in BAU scenario (the exposure level in the first 5-year time step if exposure is defined to vary through follow-up period)

Average adjusted relative risk in the whole population is calculated based on the fraction of exposed population. The non-exposed population is assumed to expose to the reference scenario level (i.e. zero or natural background exposure).

2) Calculation of morbidity risk in different exposure scenarios (and in different 5-year time steps if exposure is defined to vary through follow-up period):

DR = BDR * RR’

• DR = Annual morbidity risk in a given scenario (and in a given 5-year time step if exposure is defined to vary through follow-up period)
• RR’ = Relative risk adjusted to the exposure level in a given scenario (and in a given 5-year time step if exposure is defined to vary through follow-up period)

RR’ = Exp(ln(RR) / Unit * Exposure)

• RR = Relative risk exposure-response function
• Unit = Exposure unit to which the RR relates to
• Exposure = Exposure level in a given scenario (and in a given 5-year time steps if exposure is defined to vary through follow-up period)

3) Calculation of morbidity cases attributable to the exposure in BAU / Alternative scenario:

Attributable morbidity cases = (DR - DRReference) * Average population

• DR = Annual morbidity risk in a given 5-year time step in BAU/Alternative scenario
• DR_Reference = Annual morbidity risk in the Reference scenario (i.e. zero or natural background exposure level)
• Average population = Average number of population in a given 5-year time step in BAU/Alternative scenario

For morbidity endpoints for which the exposure-response function applied is an absolute risk (AR) function:

Attributable morbidity cases = (Attributable morbidity risk - Attributable morbidity riskReference) * Average population

• Attributable morbidity risk = Annual morbidity risk attributable to the exposure in a given exposure scenario
• Attributable morbidity risk_Reference = Annual morbidity risk attributable to the exposure in Reference scenario (i.e. zero or natural background exposure level)
• Average population = Average number of population in a given scenario, age-category and 5-year time step

Attributable morbidity risk = AR / Unit * Exposure * Pop frac

• AR = Absolute risk exposure-response function
• Unit = Exposure unit to which the RR relates to
• Exposure = Exposure level in a given scenario (and in a given 5-year time steps if exposure is defined to vary through follow-up period)
• Pop frac = Fraction of exposed population

When starting point for the assessment is 'Health outcome scenarios':

If input for morbidity outcome calculation is selected to be no. of cases, the input as such gives the number of morbidity cases attributable to the exposure / risk factor of interest. If the input for morbidity outcome calculation is selected to be percentage change, the attributable morbidity cases is calculated as follows:

1) Calculation of morbidity risk in different health outcome scenarios:

Morbidity risk in BAU and Alternative scenarios:

DRBAU/Alternative = Morbidity / Population + Morbidity / Population *  AFMorbidity data * Morbidity change / 100

• DR_{BAU/Alternative} = Morbidity risk in Business-as-usual (BAU) / Alternative scenario
• Morbidity = Annual morbidity based on the morbidity input data
• Population = Population based on the population input data
• AF_{Morbidity data} = Fraction of morbidity cases attributable to the exposure/risk factor of interest in the morbidity input data
• Morbidity change = Percentage change in attributable morbidity risk in BAU / Alternative scenario

Morbidity risk in Reference scenario:

DRReference = Morbidity / Population * (1 - AFMorbidity data)

• DR_Reference = Morbidity risk in Reference scenario
• Morbidity = Annual morbidity based on the morbidity input data
• Population = Population based on the population input data
• AF_{Morbidity data} = Fraction of morbidity cases attributable to the exposure/risk factor of interest in the morbidity input data

2) Calculation of morbidity cases attributable to the exposure / risk factor in different age-categories and 5-year follow-up time in BAU / Alternative scenario:

Attributable morbidity cases = (DRBAU/Alternative - DRReference) * Average population

• DR_{BAU/Alternative} = Annual morbidity risk in a given age-category and 5-year time step in BAU/Alternative scenario
• DR_Reference = Annual morbidity risk in a given age-category in the Reference scenario (i.e. zero or natural background exposure level)
• Average population = Average number of population in a given age-category and 5-year time step in BAU/Alternative scenario

Years of life lost due to disability (YLD)

YLD = Attributable morbidity cases * Duration * Severity * Age weight * PV life year

• Attributable morbidity cases = Attributable morbidity cases in a given age-category and 5-year time follow-up time step
• Duration = Duration for one morbidity case (years)
• Severity = Disability severity weight for a given morbidity
• Age weight = Age weight for a given age-category
• PV Life year = Present value of a life year lived in a given 5-year time step

Model description: Calculation of EBD from BoD

Summary

Years of life lost due to mortality or disease caused by an environmental exposure / risk factor (EBD) are modelled based on burden of disease (BoD) input data and population attributable fraction -method. Input data for population, mortality, morbidity, severity and duration of health endpoints, age weighting or time discount factor is not required, as this information is already contained in the burden of disease data.

It should be noted that the environmental burden of disease (in business-as-usual (BAU) or in a theoretical alternative exposure scenario) is modelled solely in regards to the time period and population represented by the input BoD data. Hence, this modelling approach does not allow for simulation of future changes in the environmental burden of disease brought upon by changes in population structure.

This chapter provides a general overview of the modeling principles applied in the Impact calculation tool. A detailed description for the code in the different calculation nodes in the model can be found here: Impact Calculation Tool code description.

1) Calculation of a baseline burden of disease (BoD), i.e. a (theoretical) burden of disease for a given mortality/morbidity endpoint in the absence of the exposure of interest:

BBoD = BoD * (1 - AFBoD data)

• BBoD = Burden of disease in the absence of the exposure / risk factor of interest
• BoD = Burden of disease (YLL or YLD depending on the endpoint of interest) based on the BoD input data
• AF_{BoD data} = Fraction of the burden of disease that is attributable to the exposure / risk factor in BAU scenario

AFBoD data = (RR’BAU -1) / RR’BAU

• RR’_BAU = Relative risk adjusted to the exposure level in BAU scenario.

RR’BAU = Exp(ln(RR) / Unit * ExposureBAU)

• RR = Relative risk per unit of exposure
• Unit = Exposure unit
• Exposure_BAU = Exposure level in BAU scenario

Average adjusted relative risk in the whole population is calculated based on the fraction of exposed population. The non-exposed population is assumed to expose to the reference scenario level (i.e. zero or natural background exposure).

2) Calculation of burden of disease in different exposure scenarios:

BoD = BBoD * RR’

• RR’ = Relative risk adjusted to the exposure level in a given scenario.

RR’ = Exp(ln(RR) / Unit * Exposure)

• RR = Relative risk exposure-response function
• Unit = Exposure unit to which the RR relates to
• Exposure = Exposure level in a given scenario

3) Calculation of environmental burden of disease (EBD) in BAU / Alternative scenario:

EBD = BoD - BoDReference

• BoD = Burden of disease in BAU / Alternative scenario
• BoD_Reference = Burden of disease in the Reference scenario (i.e. zero or natural background exposure level)

Step-by-step user instructions

Analytica software and ICT model technicalities

To be able to run the Impact Calculation Tool, you need to install Analytica software to your computer. Analytica installer can be downloaded from lumina.com. The full use of the software requires a license. However, a free Analytica player is also available. The free Analytica player lets you review and run the ICT model without having to purchase a license. With the Player edition, you can change designated inputs, run the model, view results, and examine selected model diagrams and variables. However, it does not let you make changes other than to selected inputs, or save models.

To use Analytica software, you need the following minimum configuration:

• Intel 486-66 MHz or better (Pentium 500 MHz+ or AMD Athlon recommended).
• 30 MB disk space
• 256 MB RAM (2 GB recommended for large models)
• 8-bit color display
• Windows XP, Server 2003, Server 2008, Vista, or Windows 7.

It helps to have a faster CPU, and, especially, more RAM for large models. Analytica will benefit from up to 3 GB RAM.

The Impact calculation Tool -model can be downloaded from this link: File:Impact Calculation Tool.ana

The latest model version is listed on the very top of the page. A detailed description for the code in the different calculation nodes in the model can be found here: Impact Calculation Tool code description.

The Impact Calculation tool can be operated simply from the user interface. To find detailed instructions on how to view the model and it's outputs, go to

Help → User guide → Chapter 1: Examining a Model and Chapter 2: Result Tables and Graphs

Running the Impact Calculation Tool

Assessment boundaries

Starting point for the assessment

There are three possible approaches, i.e. starting points, for conducting an environmental health impact assessment with ICT. Selection of the suitable starting point depends on the type of information and data that is available regarding the baseline health conditions in the population of interest and the quantitative relationship between exposure and the health endpoints of interest.

1) Exposure scenarios

Quantification of health impacts requires data on:

• Exposure in alternative scenarios
• Exposure-response functions (relative risk or absolute risk) for mortality/morbidity endpoints of interest
• Baseline data for annual mortality/morbidity incidence/prevalence in the population

Life table modeling is applied in the quantification of health impacts. Health impact outcomes include disability adjusted life years (DALYs), changes in life expectancy and number of attributable deaths and morbidity cases. Impacts can be modeled for a follow-up period of 1 to 100 years beginning from the start year.

2) Health outcome scenarios

Quantification of health impacts requires data on:

• Number or percentage of annual deaths/morbidity cases attributable to the exposure/hazard in alternative scenarios
• Baseline data for annual mortality/morbidity incidence/prevalence in the population

Life table modeling is applied in the quantification of health impacts. Health impact outcomes include disability adjusted life years (DALYs) and changes in life expectancy. Impacts can be modeled for a follow-up period of 1 to 100 years beginning from the start year.

3) Total burden of disease

Quantification of health impacts requires data on:

• Exposure in alternative scenarios
• Exposure-response functions (relative risk) for mortality/morbidity endpoints of interest
• Burden of disease data for mortality/morbidity endpoints of interest

The burden of disease attributable to the exposure, i.e. the so-called environmental burden of disease (EBD), is calculated based on the BoD input data. The BoD data is given in DALYs (or more specifically YLL and YLD). This data already includes information on the population structure, years of life lost due to mortality impacts and duration and severity of the morbidity impacts. Therefore, less input data is required and life table modeling is not needed. Health impact outcomes include disability adjusted life years (DALYs). Impacts are calculated for the follow-up period represented by the BoD input data.

Mortality endpoints

Define the mortality endpoints of interest.

If the selected starting point for the assessment is Exposure scenarios or Health outcome scenarios and if the list of mortality endpoints of interest does not cover all causes of mortality, then the list has to be completed with a class other causes of death. This is because life table modeling requires information on the total mortality risk in the population.

Note! If more than one endpoint is listed (i.e. the endpoint of interest is something else than all-cause mortality (natural and accidental)), the endpoint sub-categories should not be overlapping. Overlapping endpoints will result in overestimation of the total mortality risk, erroneous population projection and double counting in the health impact estimates.

If the starting point for the assessment is Total burden of disease, then the list should cover only the specific mortality endpoints of interest. This is because ICT does not apply life table modeling in this approach for quantification of health impacts and, hence, no information is needed on the total mortality risk.

Morbidity endpoints

Define the morbidity endpoints of interest. If more than one endpoint is listed, the endpoints should not be overlapping to avoid double counting in the health impact estimates.

Sex-specific assessment

Select whether or not you want to conduct sex-specified impact assessment simultaneously for males and females. If simultaneous sex-specific assessment is conducted, input data has to be provided separately for males and females.

Assessment start year

Define the first year of the assessment follow-up period. Population projection will begin from this year. Start year is defined only if the starting point for the assessment is Exposure scenarios or Health outcome scenarios.

Follow-up period

Define the number of follow-up years for which the health impacts are modeled. Number of follow-follow-up years can be 1 or any number between 1 and 100 divisible by five. This is because the time step in the population projection is five years. Population projection is always made for a 100 year period, and the life expectancy estimates are modeled based on this. However, DALYs (YLL & YLD) and attributable deaths and morbidity cases are only calculated for the follow-up period defined by the user.

Number of follow-up years is defined only if the starting point for the assessment is Exposure scenarios or Health outcome scenarios. If the starting point is Total burden of disease, the impacts are calculated for the time period represented by the BoD input data.

Note! If the assessment boundaries are changed after providing the required input data, the input data tables need to be checked and updated as necessary.

Input data (Assessment starting point: Exposure scenarios or Health outcome scenarios)

Note! Data can be inputted from Excel using copy-paste function.

Target population data

Population

Population data is provided in 1-year age intervals

Birth rate

Providing data for annual number of births is optional, and depends on the intended target population for which the health impacts are modeled. If births are omitted, the health impacts are modeled only for the population alive in the first year of the assessment (i.e. the population cohort represented by the input data). If data for annual births is provided, health impacts are also modeled in the population born during the follow-up period.

Mortality data

Mortality data refers to the annual number of deaths in the business-as-usual (BAU) scenario in the beginning of the assessment. Data is provided for all listed causes of death in 1-year age intervals.

Mortality input data is used with the population input data to determine the mortality risk in the BAU scenario and the impact of the environmental exposure on the current mortality risk. Hence, the mortality data should be representative of the exposure level in the BAU scenario in the beginning of the assessment.

Morbidity data

Morbidity data refers to the annual number of morbidity cases in the business-as-usual (BAU) scenario in the beginning of the assessment. Data is provided for all listed causes of death in 1-year age intervals.

Note! Morbidity data is only required for those morbidity endpoints for which the applied exposure-response function is a relative risk (RR).

Morbidity data can be incidence or prevalence data depending on the nature of the RR exposure-response function applied for the endpoint.

Exposure scenarios: Exposure data

The impact calculation tool is designed for evaluation of health impacts of chronic exposures, and, therefore, exposure levels can only be defined on an average annual level. The model is not well suited for evaluation of health impacts of acute exposures, because modeling of acute impacts requires, in principle, exposures and baseline mortality/morbidity risk to be defined on a daily level. However, the model can be used for assessment of acute impacts under the assumption that the exposure and baseline mortality/morbidity risk do not vary significantly on a daily level. However, these types of assessments should be approached with caution

First, select whether or not you want to define follow-up year or age-specific exposure levels for different scenarios. Exposure can be defined to change throughout the follow-up period in five-year time steps. Age-specific exposure can be defined for 5-year age groups.

Next, according to the above selections, insert the annual average exposure level in different scenarios into the correct table.

• Exposure level in the BAU scenario should reflect the true or expected exposure conditions in the population given the current state of the world.
• Exposure level in the alternative scenario should reflect the estimated exposure level after some change in the current state of the world
• Exposure level in the reference scenario should be set to zero or natural background exposure level.

The exposure level defined for a given time period is assumed to be immediately and fully reflected in the mortality/morbidity risk during that period. Hence, if the mortality/morbidity risk during a specific time period is considered to be a result from exposure during earlier or longer time period (as in case of latent health impacts), this should be reflected in the exposure level defined for the time period in question.

In case the exposure level is set to vary throughout the follow-up period and the follow-up period is less than 100 years, exposure for the rest of the 100 year population projection is set to stay on the level it is in the end of the follow-up period.

If health impacts occur only after some threshold exposure level is exceeded, the defined exposure levels should reflect the threshold exceedance in different scenarios.

In case of a categorical exposure estimate (exposure for a given person is either yes or no), the population exposure level in different scenarios should be defined as the fraction of the total population that is exposed (e.g. 1 = everybody is exposed, 0.5 = 50% of the population is exposed).

Next, define the fraction of total population that is assumed to expose to the defined exposure level (1=everybody is exposed, 0.5=50% of the population is exposed). In BAU and alternative scenarios, the rest of the population is assumed to expose to the reference scenario exposure level. Same fraction is assumed for the whole follow-up period and all age-groups.

Note! In case the exposure estimate is of a categorical type (yes/no), the fraction should be set to 1 because the percentage of exposed population has already been defined above.

Exposure scenarios: Exposure-response functions

In case of mortality endpoints, select whether you want to assess acute or chronic impacts. As explained above, the Impact Calculation Tool is designed for evaluation of health impacts of chronic exposures and is not well suited for evaluation of impacts from acute exposures. However, the model can be used for assessment of acute impacts under the assumption that the exposure and baseline mortality/morbidity risk do not vary significantly on a daily level. The acute/chronic selection affects the way exposure is assessed to affect average annual mortality risk in the population and, hence, the years of life lost (YLL) due to these impacts. Chronic impacts are assumed to be reflected in the population mortality risk, and the years of life lost are calculated based on this effect. In contrast, acute impacts are considered to represent mortality displacement, i.e. the so-called harvesting effect, and, therefore, are not reflected in the population mortality risk. In case of acute effects, the loss of life years is calculated based on the annual number of deaths and an average loss of life due to these deaths as defined by the user. The chronic/acute assumption applies to all of the evaluated mortality endpoints. Hence, if both chronic and acute mortality impacts are to be assessed, they need to be modelled in separate model runs.

In case of both mortality and morbidity impacts, select whether or not you want to define age-specific exposure-response functions.

Next, according to the above selection on the age-specificity of the applied ERFs, type in or copy-paste exposure-response functions into the correct table. If Age-specific mortality/morbidity ERFs are applied for some but not all endpoints, all ERFs should nevertheless be listed in the 'Age-specific mortality/morbidity ERF' -table.

Applied ERFs can be in the form of relative risk (RR) or absolute risk (AR). However, only one type of ERF should be defined for a given endpoint. RRs are defined on the 'Relative risk' –sheet in the input table. In case there is no response or a RR function is not applied, value 1 should be listed. ARs are defined on the 'Absolute risk' –sheet of the input table. If there is no response or an AR function is not applied, value 0 should be listed.

Note! The applied ERFs should represent the impact of the evaluated exposure level on the annual mortality/morbidity risk. Hence, lifetime risk functions are not suitable to be used in the model as such, but instead need to be converted to annual risk functions. To minimize uncertainty in the impact calculation, the applied ERFs should be compatible with the defined endpoints.

Next, define the exposure unit to which the applied ERF relates to. E.g, in case of mortality impacts of PM2.5 exposure, the applied RR relative risk could be 1.06 per 10 µg/m3, and the unit of exposure would be 10.

For mortality impacts, in case acute impacts are assessed instead of chronic impacts, define the assumed average loss of life due to one premature death attributable to the exposure in different age groups.

Health outcome scenarios: Health outcome data

Mortality outcome data

First, define the age-specific fraction of annual deaths that is attributable to the risk factor of interest in the mortality input data, e.g.

0 = None of the deaths in the input data are caused by the risk factor of interest 
0.5 = 50% of the deaths in the input data are caused by the risk factor of interest

This information with the mortality and population input data is used to determine the mortality risk attributable to the risk factor of interest in BAU scenario in the beginning of the assessment follow-up period.

Next, select whether or not you want to define follow-up year -specific input data for mortality outcome calculation. In case of follow-up year -specific input, the input data can be varied throughout the assessment follow-up period in 5-year intervals.

According to the selection above, type in or copy-paste mortality outcome input data into the correct table. The required input is a percentage change in the mortality risk attributable to the risk factor of interest in BAU and Alternative scenarios compared to the attributable mortality risk in BAU scenario in the beginning of the assessment follow-up period, e.g.

5 = 5% increase the attributable mortality risk
-5 = 5% decrease in the attributable mortality risk 

Morbidity outcome data

First, select the type of input data you want to provide for the morbidity outcome calculation. Input data can be in the form of:

• Percentage change: % increase/decrease in the morbidity risk attributable to the risk factor of interest in BAU and Alternative scenarios compared to the attributable morbidity risk in BAU scenario the beginning of the assessment follow-up period.
• No. of cases: number of morbidity cases attributable to the risk factor of interest in BAU and Alternative scenarios.

If the selected type of input is 'precentage change', provide the following input data:

• Morbidity data: annual number of morbidity cases in the beginning of the assessment follow-up period in BAU scenario
• Attributable fraction: define the age-specific fraction of morbidity cases that is caused by the risk factor of interest in the above morbidity data, e.g.

0 = None of the morbidity cases in the input data are caused by the risk factor of interest 
0.5 = 50% of the morbidity cases in the input data are caused by the risk factor of interest

This information with the population input data is used to determine the morbidity risk attributable to the risk factor of interest in BAU scenario in the beginning of the assessment follow-up period.

Next, select whether or not you want to define follow-up year -specific input for morbidity outcome calculation. In case of follow-up year -specific input, the input data can be varied throughout the assessment follow-up period in 5-year intervals.

According to the selection above, type in or copy-paste input data for morbidity outcome into the correct table. If the input for morbidity outcome calculation is 'Precentage change', insert a precent change in the morbidity risk attributable to the risk factor of interest in BAU and Alternative scenarios compared to the attributable morbidity risk in BAU scenario the beginning of the assessment follow-up period, e.g.

5 = 5% increase in attributable morbidity risk
-5 = 5% decrease in attributable morbidity risk

If the input for morbidity outcome calculation is 'No. of cases', insert an annual number of morbidity cases attributable to the risk factor of interest in BAU and Alternative scenarios, e.g.

0 = 0 attributable morbidity cases annually
50 = 50 attributable morbidity cases annually

Morbidity data

Duration

Select whether or not you want to apply age-specific durations of morbidity.

Next, according to the selection above, insert the duration data into the correct table. If Age-specific duration of morbidity = Yes then durations for all morbidity endpoints (age-specific or not) should be inserted in the Age-specific duration of morbidity -table.

Duration is given in years. If the applied exposure-response function refers to morbidity incidence in the population, duration can be anything up to the age-specific life expectancy of the individuals suffering the morbidity. If the exposure-response function refers to morbidity prevalence in the population, duration should be set to one year.

Severity weight

Select whether or not you want to apply age-specific severity weights for morbidity endpoints.

Next, according to the selection above, insert the severity weights into the correct table. If Age-specific severity weight = Yes then weights for all morbidity endpoints (age-specific or not) should be inserted in the Age-specific severity weight -table.

Severity weight for a given morbidity endpoint should be a number between 0 and 1 (0 = perfect health, 1 = death). See Disability weights for more information.

Time discount rate

Define the annual discount rate applied in the valuation of future gains or losses of life. Discount rate is given as a percentage.

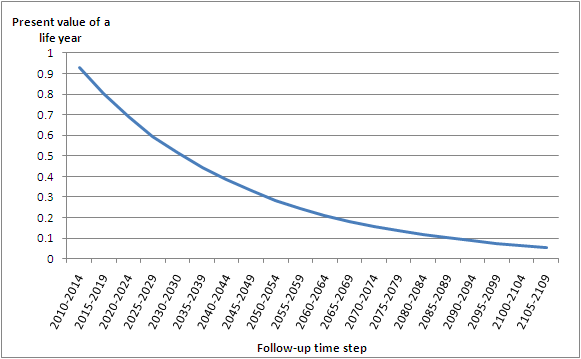
Based on the annual discount rate, the present value (PV) of life years gained or lost during the follow-up period is determined. Discounting begins from the start year of the assessment, i.e. the start year is always assumed to be the present time. The PV of a life year during a given 5-year time step is based on the PV in the middle of the 5-year period. An example of the effect of time discounting on the value of future life is given in figure 1. If time discounting is not applied, i.e. life years lost or gained during any given time step is valued the same, the discount rate should be set to 0.

Figure 1. Present value of a future life year assuming a 3% annual discount rate (assessment start year 2010).

Age weighting

Select whether or not to use age weighting in the valuation of life lost or lived with morbidity.

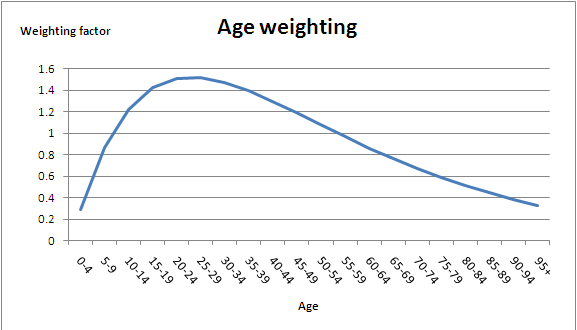
If age weighting is applied, life lived at a given age is weighed with the standard age weights applied in the WHO Global Burden of Disease studies (see: Murray 1994. Quantifying the burden of disease: the technical basis for disability adjusted life years. Bulletin of the World Health Organization 72, 429-445).

Age weights are calculated based on the function:

Cxe^(-bx)
C = 0.1658
x = age in years
b = 0.04

Figure 2. Age weighting function

Health impact outcomes (Assessment starting point: Exposure scenarios or Health outcome scenarios

Specify how outcomes are calculated

Select the outcome of interest

1) EBD

Health impacts caused by the exposure/risk factor of interest in BAU and Alternative scenarios compared to the Reference scenario. In case the assessment starting point is 'Exposure scenarios', the Reference scenario represents health impacts in zero or natural background exposure level as defined by the user. In case the starting point for the assessment is 'Health outcome scenarios', the Reference scenario represents health impacts at a zero risk factor level.

2) Change in EBD

Increase/decrease in the health impacts in Alternative exposure/risk factor scenario compared to BAU scenario

Select the approach for calculating YLL

Life tables

YLL in BAU and Alternative scenarios is calculated based on the population projections and the difference in the number of life years lived during the follow-up period in the BAU/Alternative scenario compared to the hypothetical Reference scenario (zero or natural background exposure level).

It should be noted, that in this approach the total amount of life lost due to a given premature mortality case is NOT allocated to the year during which the death occurs, but to all future follow-up years when the life would have taken place if death would not have occurred.

Attributable deaths

YLL is calculated based on year and age-specific attributable deaths and age-specific life-expectancy in the Reference scenario. Hence, the total life lost due to a given premature mortality case is allocated to the year when the death takes place.

Note! In case of morbidity incidence endpoints, the total life lost due to disability caused by a morbidity case is allocated to the year when the morbidity appears, regardless of the selected approach for the calculation of YLL

Impacts on life-expectancy

Life expectancy in birth cohort

Gives the average life-expectancy in a birth cohort in different scenarios. The cohort is assumed to expose to the level defined for the scenario through the entire lifetime. If the exposure varies through the assessment follow-up period, and the follow-up period < 100 years, the exposure level and the resulting total mortality risk after the follow-up period is assumed to stay on the level of the last follow-up time step.

Loss of life expectancy for birth cohort

Gives the average loss of life expectancy (years) in a birth cohort in BAU and Alternative scenarios compared to the Reference scenario.

Age-adjusted life expectancy

Gives the average age-specific life-expectancy for 5-year age groups in different scenarios. If the exposure varies through the assessment follow-up period, and the follow-up period < 100 years, the exposure level and the resulting total mortality risk after the follow-up period is assumed to stay on the level of the last follow-up time step.

Loss of age-adjusted life expectancy

Gives the average loss of age-specific life expectancy (years) in BAU and ALternative scenarios compared to the Reference scenario.

Attributable mortality and morbidity counts

Mortality, total

Gives the total number of deaths for different mortality endpoints attributable to the exposure during the assessment follow-up period.

Mortality, specified

Gives the number of attributable deaths in different 5-year age groups and 5-year follow-up time steps.

Morbidity, total

Gives the total number of morbidity cases for different morbidity endpoints attributable to the exposure during the assessment follow-up period.

Morbidity, specified

Gives the number of attributable morbidity cases in different 5-year age groups and 5-year follow-up time steps.

Burden of disease measures

YLL, total

Gives the total number of life years lost due to premature mortality attributable to the exposure during the assessment follow-up period.

YLL, specified

Gives the number of life years lost due to premature mortality in different 5-year age groups and 5-year follow-up time steps.

YLD, total

Gives the total number of healthy life years lost due to disability attributable to the exposure during the assessment follow-up period.

YLD, specified

Gives the number of healthy life years lost due to disability in different 5-year age groups and 5-year follow-up time steps.

DALY, total

Gives the total loss of disability adjusted life years attributable to the exposure during the assessment follow-up period.

DALY, specified

Gives the loss of disability adjusted life years in different 5-year age groups and 5-year follow-up time steps.

Input data (Assessment starting point: Total burden of disease)

Total burden of disease data

Burden of disease (BoD) data should be given as life years lost due to mortality (YLL) or disability (YLD) depending on the endpoint of interest. Type in or copy-paste the data into the correct table.

Exposure data

First, select whether or not you want to define age-specific exposure levels.

Next, according to the above selection, insert the exposure data into the correct table. Exposure in different scenarios (BAU, alternative, reference) should be given as an average annual exposure level.

• Exposure level in the BAU scenario should reflect the true exposure conditions in the population at the time period represented by the input data on the burden of disease (YLL/YLD).
• Exposure level in the alternative scenario should reflect the exposure level after some change in the current state of the world.
• Exposure level in the reference scenario should be set to zero or natural background exposure level.

If health impacts occur only after some threshold exposure level is exceeded, the defined exposure levels should reflect the threshold exceedance in different scenarios.

In case of a categorical exposure estimate (exposure for a given person is either yes or no), the population exposure level in different scenarios should be defined as the fraction of the total population that is exposed (e.g. 1 = everybody is exposed, 0.5 = 50% of the population is exposed).

Next, define the fraction of total population that is assumed to expose to the defined exposure level (1=everybody is exposed, 0.5=50% of the population is exposed). In BAU and alternative scenarios, the rest of the population is assumed to expose to the reference scenario exposure level. Same fraction is assumed for all age-groups.

Note! In case the exposure estimate is of a categorical type (yes/no), the fraction should be set to 1 because the percentage of exposed population has already been defined above.

Exposure-response function

First, select whether or not you want to define age-specific exposure-response functions.

Next, type in or copy-paste exposure-response functions into the correct table.

ERFs can only be defined in the form of a relative risk (RR). ERFs need to be compatible with the defined mortality/morbidity endpoints. To avoid double counting, ERFs should not be overlapping in regard to the listed endpoints.

Note! If Age-specific mortality/morbidity ERF = 'Yes', then all ERFs (including both age-specific and general) should be listed in the 'Age-specific mortality/morbidity ERF' -table.

Next, define the exposure unit to which the ERF relates to.

Health impact outcomes (Assessment starting point: Total burden of disease)

Environmental burden of disease in BAU or in a theoretical alternative exposure scenario is modelled solely in regards to the time period represented by the input BoD data. Hence, this modelling approach does not allow for simulation of future changes in the environmental burden of disease brought upon by the changes in population structure. Any time discounting or age weighting included in the original BoD input data also apply to the EBD results.

YLL, total

Gives the total number of life years lost due to premature mortality attributable to the exposure.

YLL, specified

Gives the number of life years lost due to premature mortality in different 5-year age groups.

YLD, total

Gives the total number of healthy life years lost due to disability attributable to the exposure.

YLD, specified

Gives the number of healthy life years lost due disability in different 5-year age groups.

DALY, total

Gives the total loss of disability adjusted life years attributable to the exposure.

DALY, specified

Gives the loss of disability adjusted life years in different 5-year age groups.

See also

• File:Impact Calculation Tool.ana