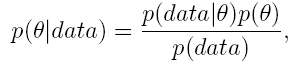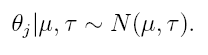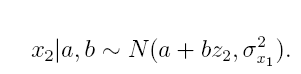Bayesian analysis: Difference between revisions
(→Bayesian meta-analysis: images added) |
(→Combining information from different types of studies: eqs as images) |
||
| Line 111: | Line 111: | ||
In this second data set we denote ambient concentration by z<sub>2</sub> and personal exposure | In this second data set we denote ambient concentration by z<sub>2</sub> and personal exposure | ||
by x<sub>2</sub>. Solution to our problem now is a model consisting of two parts. First part is | by x<sub>2</sub>. Solution to our problem now is a model consisting of two parts. First part is | ||
logistic | logistic health effect model which assumes that | ||
<center> | <center>[[Image:Logistic health effect model.PNG]]</center> | ||
| Line 121: | Line 121: | ||
<center> | <center>[[Image:Linear regression.PNG]]</center> | ||
| Line 128: | Line 128: | ||
<center> | <center>[[Image:Params a and b.PNG]]</center> | ||
| Line 138: | Line 138: | ||
<center> | <center> | ||
[[Image:To summarize.PNG]] | |||
[[Image:To summarize 2.PNG]] | |||
</center> | |||
| Line 153: | Line 148: | ||
and for parameters a and b. The posterior distribution of this model can be simulated | and for parameters a and b. The posterior distribution of this model can be simulated | ||
using MCMC methods described above. This kind of idea is applied for example in [3]. | using MCMC methods described above. This kind of idea is applied for example in [3]. | ||
== Final remarks == | == Final remarks == | ||
Revision as of 10:05, 20 April 2007
The text below is based on the review document made in the first phase of Intarese project. The original document can be found here: Bayes review
KTL (M. Hujo)
Basic ideas
Most researchers first meet with concepts of statistics through the frequentistic thinking. Bayesian statistics offers us an alternative to frequentistic methods.
Bayesian thinking and modeling is based on probability distributions. Very basic concepts in Bayesian analysis are prior and posteorior distribution. A prior distribution p(θ) summarizes our existing knowledge on θ (before data is seen). It can, for example, describe the opinion of a specialist and therefore Bayesian modelling requires that we accept the concept of subjective probability. A posterior distribution p(θ|data) describes our updated knowledge after we have seen data. A posterior is formed by combining a prior and likelihood p(data|θ) (derived using the same techniques as in frequentistic statistic) using Bayes' formula,
As we can see, this is a natural mechanism for learning, it gives a direct answer to the question: "How does data change our belief in the matter we are studying?"
From above we also see that one of the main differences between frequentist and Bayesian analyses lies in whether we use only likelihood or whether we also use prior distribution. Prior distribution allows us to make use of information from earlier studies. We summarize this information with our prior distribution and then use Bayes' formula and our own data to update our knowledge. If we do not have any previous information on the issue we are studying we may use so called uninformative prior meaning that our prior distribution does not contain much information, for example a normal distribution with large variance. As we see from Bayes' formula, the use of uninformative prior lets data define our posterior distribution.
Of course there are also differences between Bayesian and frequentistic statistics. One is the way of thinking. In frequentistic analysis the parameter θ is taken to be fixed (albeit unknown) and data is considered to be random whereas Bayesian statisticians would say that θ is uncertain and follows a probability distribution while data is taken to be fixed.
Also it is important to notice that Bayesian analysis carefully distinguishes between p(θ | data) and p(data | θ) and all inference from Bayesian analysis is based on a posterior distribution, which is a true probability distribution. Thus Baysian analysis ensures natural intepretations for our estimators and probability intervals. More on the basics of Bayesian analysis can be found for example in [1] and [2].
Markov chain Monte Carlo
In practice it is not straightforward to compute an arbitrary posterior distribution, but we can sample from it. For sampling we may use the Markov chain Monte Carlo idea which is often abbreviated MCMC. Simply the idea is to construct a Markov chain such that it has the desired posterior distribution as its limiting distribution. Then we simulate this chain and get a sample from the desired distribution. Perhaps the most commonly used software writen for MCMC is called BUGS which is an abbreviation of 'Bayesian statistics Using Gibbs Sampling'.
Bayesian meta-analysis
A meta-analysis is a statistical procedure in which the results of several independent studies are integrated. There are always some basic issues to be considered in meta- analysis such as the choice between using a fixed-effects model or a random-effects model, the treament of small studies and incorporation of study-specific covariates. For example, analysis of the results of a clinical trial with many health care centers involved. The centers may differ in their patient pool e.g. number of patients, overall health level and age or the quality of the health care they provide. It is widely recognized that it is important to explicitly deal with the heterogeneity of the studies through random-effects models, in which for each center there is a center-specific "true effect" included. Bayesian methods allow us to deal with these problems within a unified frame work (cf. [5]). A major advantage in Bayesian approach is the ease with which one can include study-specific covariates and that inference concerning the study-specific effects is done a natural manner through the posterior distributions. Compared to classical methods Bayesian approach, possibly, gives more complete representation of between-study heterogeneity and for sure more transparent and intuitive reporting of results. Of course the cost of these benefits is that a prior specification is required.
To shed more light on Bayesian meta-analysis, let us now give a relatively simple example. Assume that we have n studies. We are interested in average µ of the parameters θj , j = 1,..,n. Using information available from these studies we calculate a point estimator yj for parameter θj . The first stage of the hierarchical Bayesian model assumes that the point estimators conditioned on parameters are e.g. normally distributed i.e.
We can simplify this model by assuming that σj is known. This simplification does not have much effect if sample sizes for each study are large enough. As an estimator of σj we can take for example sampling variance of point estimator yj.
The second stage of our model assumes normality for θj conditioned on hyperparameters μ ja τ ,
Finally, we assume noninformative hyperpriors for μ and τ . The analysis of our meta-analysis model follows a now normal Bayesian procedure, the inference is again based on posterior distribution p(μ | data).
More reading on the applications of Bayesian meta-analysis can be found in [3] and [4].
Combining information from different types of studies
Let us now consider an example on air pollution (fine particles) and its healt effects measured by healt test. We interested in relation of personal exposure to fine particle matter and the health effect. For healt effect we have binary data y, y ~ Ber(p), given by a health test (st depression) where one indicates a health problem and zero stands for no problem. We also have data on ambient concentration of fine particle matter, denoted by variable z1, for each day of health test. What we do not have is data on personal exposure for health measurement days which we denote by x1. So there is a missing information between personal exposure and healt test. However we have another data set that connects ambient concentration to personal exposure. In this second data set we denote ambient concentration by z2 and personal exposure by x2. Solution to our problem now is a model consisting of two parts. First part is logistic health effect model which assumes that
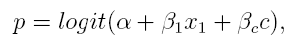
where c stands for all confounding variables required in model. Second part is a
linear regression model
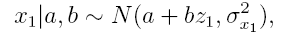
where we obtain estimates to personal exposure on health test days. Parameters a
and b are estimated from

using our second data set. One of advantage using Bayesian statistics here to analyze
relation on personal exposure and healt effect is that the model takes into account
our uncertainty of x1 in (1.1).
To summarize above we have
To complete our model we set some prior distributions for parameters ά, β1, β2
and for parameters a and b. The posterior distribution of this model can be simulated
using MCMC methods described above. This kind of idea is applied for example in [3].
Final remarks
Bayesian methods offer a rather flexible tool to combine studies and there is some software available to use with Bayesian analysis. Intepretations for Bayesian estimators and probability intervals are very natural because Bayesian analysis is based on true probability distributions. For example a Bayesian 95% probability interval has interpretation that parameter of interest µ lies in that interval with probability 0:95. Frequentistic confidence interval is a random interval meaning that if we would repeat our calculations 100 times with new data each time then, in average, 95 of our confidence intervals would contain θ.
References
[1] P. Congdon. Applied Bayesian Modelling. Wiley series in probability and statistics 2003.
[2] A. Gelman, J. B. Carlin, H. S. Stern, D.B. Rubin. Bayesian data analysis. Chap-
man & Hall 2004.
[3] F. Dominici, J. M. Samet, S. L. Zeger A measurement error model for time-series
studies of air pollution and mortality. Biostatistics (2000), 1, pp. 157-175
[4] J. M. Samet, F. Dominici, F. C. Curriero, I. Coursac, S. L. Zeger. Fine partuculate
air pollution and mortality in 20 U.S. cities. The New Enland Journal of Medicine
(2000), 342, 24, pp. 1742-1749
[5] T. Smith, D. Spiegelhalter, A. Thomas Bayesian approaches to random-effects
meta-analysis: a comparative study. Statistics in Medicine (1995) 14(24) pp. 2685-99.