Variable structure: Difference between revisions
(Causality changed to Dependencies) |
mNo edit summary |
||
| Line 19: | Line 19: | ||
* [[Clairvoyant test]] | * [[Clairvoyant test]] | ||
=== | ===Dependencies=== | ||
* [[PSSP]] | * [[PSSP]] | ||
| Line 51: | Line 51: | ||
|---- | |---- | ||
| Formula | | Formula | ||
| Formula {{ | | Formula {{reslink|Discussion on formula attribute}} is an operationalisation of how to calculate or derive the result based on ''Dependencies'', ''Data'', and ''Unit'', making a synthesis of the three. Formula uses algebra, computer code, or other explicit methods if possible. | ||
|----- | |----- | ||
| '''Result''' | | '''Result''' | ||
Revision as of 20:22, 13 July 2009
| Moderator:Nobody (see all) Click here to sign up. |
|
|
| Upload data
|
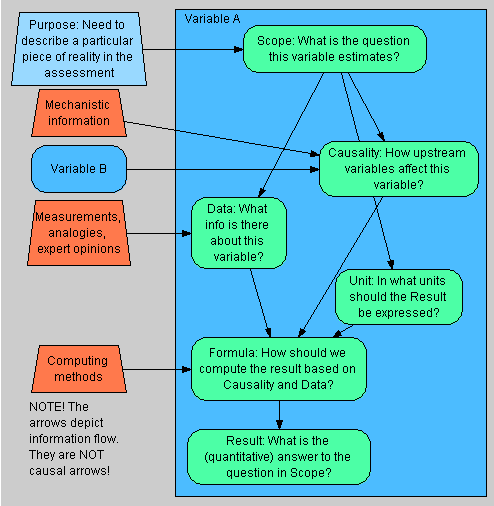
Scope
- The research question about the structure of a variable
- What is a structure of a variable such that it
- is able to systematically handle all kinds of information about the particular piece of reality that the variable is describing,
- is able to systematically describe causal relationships between variables,
- enables both quantitative and qualitative descriptions,
- is suitable for any kinds of variables, especially physical phenomena, decisions, and value judgements,
- inherits its main structure from universal objects,
- complies with the PSSP ontology,
- can be operationalised in a computational model system,
- results in variables that are independent of the assessment(s) it belongs to;
- results in variables that pass the clairvoyant test.
Definition
Data
Dependencies
Result
| Attribute | Sub-attribute | Comments specfic to the variable attributes |
|---|---|---|
| Name | ||
| Scope | This includes a verbal definition of the spatial, temporal, and other limits (system boundaries) of the variable. The scope is defined according to the use purpose of the assessment(s) that the variable belongs to. | |
| Definition | Dependencies | Dependencies R↻ tells what we know about how upstream variables (i.e. causal parents) affect the variable. Dependencies list the causal parents and expresses their functional relationships (the variable as a function of its parents) or probabilistic relationships (conditional probability of the variable given its parents). The expression of causality is independent of the data about the magnitude of the result of the variable. |
| Data | Data tells what we know about the magnitude of the result of the variable. Data describes any non-causal information about the particular part of reality that is being described, such as direct measurements, measured data about an analogous situation (this requires some kind of error model), or expert judgment. | |
| Unit | Unit describes, in what measurement units the result is presented. The units of interconnected variables need to be coherent with each other given the functions describing causal relations. The units of variables can be used to check the coherence of the causal network description. This is a so called unit test. | |
| Formula | Formula R↻ is an operationalisation of how to calculate or derive the result based on Dependencies, Data, and Unit, making a synthesis of the three. Formula uses algebra, computer code, or other explicit methods if possible. | |
| Result | A result is an estimate about the particular part of reality that is being described. It is preferably a probability distribution (which can in a special case be a single number), but a result can also be non-numerical such as "very valuable". |
In addition, it is practical to have additional subtitles on a variable page. These are not attributes, though.
- See also
- References
Specific issues related to variable attributes
In a general form, the formula can be described as
result = formula(causal parameters, data parameters, unit),
- where formula is a function (expressed as algebra or computer code for a specified software) for calculating the result using the causal parameters (information from causally upstream variables) and the data parameters (information from observed data) as input. The formula can be placed within <anacode></anacode> or <rcode><rcode>, if it is expressed as Analytica or R code, respectively.
It should be noted that the result is the distribution itself, although it can be expressed as some kind of description of the distribution, such as mean and standard deviation. The result should be described in such a detailed way that the full distribution can be reproduced from the information presented under this attribute. A technically straightforward way to do this is to provide a large random sample from the distribution.
The result may be a different number for different locations, such as geographical positions, population subgroups, or other determinants (e.g. years 2000, 2001). Then, the result is described as
R given x1,x2,...
where R is the result and x1 and x2 are defining the locations along an index (e.g. Year3). Index is a technical tool for dealing with the dimensionality of the variable. A dimension means a property along which locations are located (e.g. Time). In this case, x1 and x2 are indices along some dimensions, and particular values of x1 and x2 are locations. A variable can have zero, one, or more dimensions. Even if a dimension is continuous, it is usually operationalised in practice as a list of discrete locations. R↻
See also
References
Will appear here automatically, if cited above using the <ref></ref> tags. Additional references can also be listed here.