Epidemiological modelling: Difference between revisions
(Created page with " {{assessment}} op_fi:Epidemiologinen_malli") |
(curator added) |
||
| (58 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[op_fi:Epidemiologinen_malli]] | |||
{{method|moderator=Mnud}} | |||
{{progression class|progression=Checked|curator=THL|date=2016-03-21}} | |||
==Question== | |||
How to predict the net effectiveness of pneumococcal conjugate vaccination with a given set of serotypes when the vaccine is included in the national immunisation programme? | |||
* The focus is on the incidence of invasive pneumococcal disease (IPD) cases in different age groups covering the whole population. | |||
* The model is assumed to be valid in a population in which pneumococcal conjugate vaccination of infants has been in place for several years so that a new steady-state after vaccination has been reached. | |||
* The coverage of vaccination and vaccine efficacy against carriage are assumed to be high enough to justify the assumption of complete elimination of vaccine-type carriage among both the vaccinated and also, due to substantial herd effects, among the unvaccinated members of the population. | |||
* Vaccine-type carriage will be completely replaced by carriage of the non-vaccine types whose disease causing potential is not altered by vaccination. | |||
==Answer== | |||
The predicted reduction in the incidence of invasive pneumococcal disease (IPD) in different age groups are obtained from the serotype replacement model <ref name="optimalserotype">[http://www.ploscompbiol.org/article/info%3Adoi%2F10.1371%2Fjournal.pcbi.1003477 Nurhonen M, Auranen K (2014) Optimal Serotype Compositions for Pneumococcal Conjugate Vaccination under Serotype Replacement. PLoS Comput Biol 10(2): e1003477. doi:10.1371/journal.pcbi.1003477]</ref>. | |||
=== Computation === | |||
The following program illustrates the working of the replacement model. In its current implementation the code allows the user to specify upto 4 vaccine compositions and then displays the predicted ''number'' of IPD cases in Finland per year corresponding to these vaccines. The results are shown by serotype and by age category (<5 and 5+ year olds). Possible choices for vaccine compositions are: PCV10, PCV13, no vaccination and a user specified serotype composition. The program is based on the code in File S1 in <ref name="optimalserotype"></ref>. | |||
<br> | |||
* <big>'''<u>Instructions for user: Choose the desired vaccine compositions from the list below and then press "Run code".</u>''' | |||
You can compare 2,3 or 4 vaccine compositions. The results will be displayed on a separate tab. The default choice is PCV10 and PCV13.</big> | |||
<rcode embed=0 graphics=1 variables=" | |||
name:vac|description:Please choose the vaccines to be compared:|type:checkbox|options: | |||
'PCV10';PCV-10; | |||
'PCV13';PCV-13; | |||
'No_vaccination';No vaccination| | |||
default:'PCV10';'PCV13'| | |||
category:Scenarios| | |||
name:custom_vac|description:Do you want to specify another vaccine composition?|type:selection|options: | |||
FALSE;No; | |||
TRUE;Yes| | |||
default:FALSE| | |||
name:vac_user|description:Choose the serotypes for the user defined vaccine composition|type:checkbox|options: | |||
'1';1; | |||
'3';3; | |||
'4';4; | |||
'6A';6A; | |||
'6B';6B; | |||
'6C';6C; | |||
'7';7F; | |||
'8';8; | |||
'9N';9N; | |||
'9V';9V; | |||
'10';10; | |||
'11';11; | |||
'12';12; | |||
'14';14; | |||
'15';15; | |||
'16';16; | |||
'18C';18C; | |||
'19A';19A; | |||
'19F';19F; | |||
'20';20; | |||
'22';22; | |||
'23A';23A; | |||
'23F';23F; | |||
'33';33; | |||
'35';35; | |||
'38';38; | |||
'Oth';Other| | |||
default:'19F';'23F';'6B';'14';'9V';'4';'18C';'1';'7'| | |||
category:User defined vaccine| | |||
category_conditions:custom_vac;TRUE" | |||
> | |||
library(OpasnetUtils) | |||
library(ggplot2) | |||
#vacc1 <- vac | |||
#vacc2 <- custom_vac | |||
if(custom_vac) { | |||
vac <- c(vac, "UserDefined") | |||
} | |||
if (length(vac) == 0) stop("No vaccines were specified.") | |||
user_args <- list( | |||
Scenario = vac | |||
) | |||
# Ulkoinen säilö datalle jollain sivulla? | |||
temp <- data.frame( | |||
Vaccine = rep(c("PCV10", "PCV13"), c(9, 12)), | |||
Serotype = c('19F', '23F', '6B', '14', '9V', '4', '18C', '1', '7', | |||
'19F', '23F', '6B', '14', '9V', '4', '18C', '1', '7', '3', '6A', '19A' | |||
) | |||
) | |||
user_args$Vaccines <- temp[temp$Vaccine %in% user_args$Scenario, ] | |||
if(custom_vac) { | |||
user_args$Vaccines <- rbind( | |||
user_args$Vaccines, | |||
data.frame(Vaccine = "UserDefined", Serotype = vac_user) | |||
) | |||
} | |||
#if(!exists("servac_user")) servac_user <- c('19F', '23F', '6B', '14', '9V', '4', '18C', '1', '7') | |||
objects.latest("Op_fi4305", code_name = "alusta") # [[Pneumokokkirokote]] | |||
objects.latest("Op_en6007", code_name = "answer") # [[OpasnetUtils/Drafts]] | |||
openv.setN(100) | |||
## Read the annual IPD and carriage incidence data. | |||
## The 0 entries in IPD and carriage data are replaced by small values. | |||
serotypes<-c( | |||
"19F", "23F", "6B", "14", "9V", "4", "18C", "1", "7", | |||
"6A", "19A", "3", "8", "9N", "10", "11", "12", "15", | |||
"16", "20", "22", "23A", "33", "35", "38", "6C", "Oth") | |||
car_under5<-c( | |||
156030, 156030, 126990, 41200, 22290, 12830, 10130, 10, 14180, | |||
54940, 24320, 12160, 1350, 20940, 4050, 72270, 10, 33100, | |||
3380, 1350, 12160, 3380, 680, 30400, 4050, 27470, 24320 ) | |||
car_over5<-c( | |||
168100, 314800, 256700, 209800, 114100, 62500, 200700, 100, 100, | |||
158800, 54900, 30800, 8800, 8800, 20800, 97700, 100, 100, | |||
191900, 25200, 72500, 22000, 100, 71300, 100, 79400, 330100 ) | |||
ipd_under5<-c( | |||
7.78, 7.88, 24.39, 20.76, 2.91, 2.91, 6.64, 0.31, 3.02, | |||
3.94, 9.88, 1.25, 0.10, 0.83, 0.41, 0.42, 0.21, 1.98, | |||
0.21, 0.01, 0.93, 0.10, 0.42, 0.31, 0.42, 0.01, 0.73 ) | |||
ipd_over5<-c( | |||
28.51, 53.72, 29.53, 99.43, 43.07, 76.99, 24.39, 6.58, 46.88, | |||
17.42, 20.54, 55.04, 11.21, 25.20, 6.28, 12.76, 13.89, 9.18, | |||
4.73, 3.29, 29.03, 4.40, 5.64, 12.41, 1.43, 5.50, 11.20 ) | |||
## Combine the data into 2 matrices of dimension 27*2: | |||
IPD<-cbind(ipd_under5, ipd_over5) | |||
Car<-cbind(car_under5, car_over5) | |||
## Row numbers corresponding to the 3 different PCV formulations | |||
## in matrices IPD and Car. Note: there is no serotype 5 in our data. | |||
pcv7rows<-seq(7); pcv10rows<-seq(9); pcv13rows<-seq(12) | |||
## Example S1.2A: Calculate the predicted incidence of IPD for the non-vaccine | |||
## types(NVTs) under PCV13. The predictions are calculated separately for the | |||
## two age classes. These are the values reported on the bottom panel in | |||
## Figure 2 (there given as per 100K incidences). | |||
postvacc <-Vaccination(IPD,Car,VT_rows=pcv13rows,p=1,q=1) | |||
## Example S1.2B: Decrease in IPD incidence after adding a single new serotype | |||
## to PCV13 separately for the two age categories. | |||
next_under5<-NextVT(IPD[,1],Car[,1], VT_rows=pcv13rows,p=1) | |||
next_over5 <-NextVT(IPD[,2],Car[,2], VT_rows=pcv13rows,p=1) | |||
# Nämä taulukot kannattaisi transposata niin näyttäisivät siistimmiltä. | |||
## Example S1.3A: The optimal sequence for under 5 year olds when replacement is 100%. | |||
## The output shows the decreases in IPD incidence for each step, | |||
## corresponding to Figure 5(C). The last serotype (row 27, the category "Other") | |||
## is excluded from any vaccine composition but is taken into account as a | |||
## replacing serotype at each stage. | |||
opt<-OptimalSequence(IPD[,1],Car[,1],VT_rows=0,Excluded_rows=27,p=1.0,HowmanyAdded=20) | |||
## Example S1.3B: The optimal sequence for the whole population when | |||
## replacement is 50% and the current composition includes the PCV7 serotypes. | |||
opt<-OptimalSequence(IPD,Car, VT_rows=pcv7rows,Excluded_rows=length(serotypes), | |||
p=0.5,HowmanyAdded=17) | |||
################################### | |||
## Read the annual IPD and carriage incidence data. | |||
## The 0 entries in IPD and carriage data are replaced by small values. | |||
IPD <- Ovariable("IPD", ddata = "Op_fi4305.pneumokokki_vaestossa") | |||
IPD@data <- IPD@data[IPD@data$Observation == "Incidence" , colnames(IPD@data) != "Observation"] | |||
Car <- Ovariable("Car", ddata = "Op_fi4305.pneumokokki_vaestossa") | |||
Car@data <- Car@data[Car@data$Observation == "Carrier" , colnames(Car@data) != "Observation"] | |||
servac <- merge(data.frame(Vaccine = user_args$Scenario), data.frame(Serotype = serotypes)) | |||
servac <- merge( | |||
data.frame(user_args$Vaccines, Result = 1), | |||
servac, | |||
all.y = TRUE | |||
) | |||
servac$Result <- as.numeric(!is.na(servac$Result)) | |||
servac <- Ovariable( | |||
"servac", | |||
data = servac | |||
) | |||
#data.frame( | |||
#Vaccine = rep(c("Current", "New"), each = length(serotypes)), | |||
#Serotype = serotypes, | |||
#Result = as.numeric(c( | |||
# serotypes %in% c("19F", "23F", "6B", "14", "9V", "4", "18C", "1", "7"), | |||
# serotypes %in% servac_user | |||
# )) | |||
#)) | |||
p_user<-q_user<-adultcarriers<-1 | |||
p <- Ovariable("p", data = data.frame(Result = p_user)) | |||
q <- EvalOutput(Ovariable("q", data = data.frame(Result = q_user))) | |||
# EvalOutput must be used because q is mentioned twice in the code and there will otherwise be a merge mismatch. | |||
# The true number of adult carriers may actually be larger than estimated. This adjusts for that. | |||
Car <- Car * Ovariable("adjust", data = data.frame(Age = c("Under 5", "Over 5"), Result = c(1, adultcarriers))) | |||
VacCar <- EvalOutput(VacCar) | |||
VacIPD <- EvalOutput(VacIPD) | |||
if (1==0) { | |||
cat("servac\n") | |||
oprint(summary(servac)) | |||
cat("Number of carriers\n") | |||
oprint(summary(VacCar)) | |||
cat("Incidence of invasive pneumococcal disease.\n") | |||
oprint(summary(VacIPD)) } | |||
if("Iter" %in% colnames(VacCar@output)) N <- max(VacCar@output$Iter) else N <- 1 | |||
if (1==0) {ggplot(VacCar@output, aes(x = Serotype, weight = result(VacCar) / N, fill = Vaccine)) + geom_bar(position = "dodge") + theme_gray(base_size = 24) + | |||
labs(title = "Carriers", y = "Number of carriers in Finland") } | |||
ggplot(VacIPD@output, aes(x = Serotype, weight = result(VacIPD) / N, fill = Vaccine)) + geom_bar(position = "dodge") + theme_gray(base_size = 24) + | |||
labs(title = "Incidence of invasive pneumococcal disease", y = "Number of cases per year") | |||
ggplot(VacIPD@output, aes(x = Vaccine, weight = result(VacIPD) / N, fill = Age)) + geom_bar(position = "stack") + theme_gray(base_size = 24) + | |||
labs(title = "Incidence of invasive pneumococcal disease", y = "Number of cases per year") | |||
</rcode> | |||
==Rationale== | |||
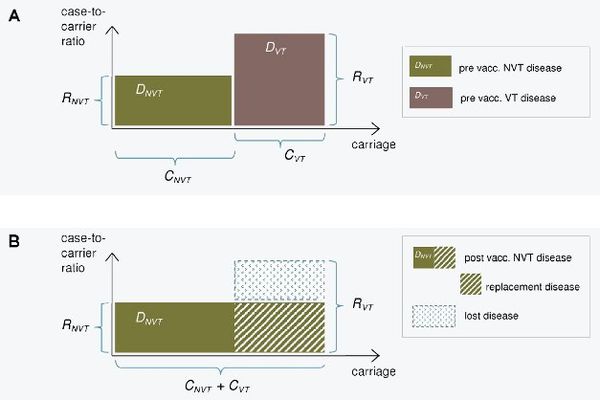
The epidemiological model for pneumococcal carriage and disease is based on the assumption that vaccination completely eliminates vaccine-type carriage in the vaccinated population and that vaccine-type carriage is completely replaced by non-vaccine-type carriage. The implications of this replacement on the decrease or increase in pneumococcal disease then depend on the disease causing potential of the replacing types compared to that of the replaced types. To predict the incidence of post-vaccination disease only pre-vaccination data on serotype-specific carriage and disease are used. | |||
The consequences of serotype replacement in the model depend on two key assumptions regarding the new steady-state after vaccination: | |||
# the relative serotype proportions among the non-vaccine types are not affected by vaccination (proportionality assumption); | |||
# the case-to-carrier ratios (the disease causing potentials) of individual serotypes remain at their pre-vaccination levels. | |||
The implications of vaccination on disease incidence are assumed to be solely due to the elimination of vaccine type carriage and its replacement by non vaccine-type carriage. An exception to this is when protective efficacy against disease without any efficacy against carriage is assumed for certain serotypes (a feature to be added). | |||
[[File:Model_kuva_simplified2.jpg|thumb|center|600px|'''Figure 1. Illustration of the replacement model.''' The incidence of pneumococcal carriage (x-axis) and case-to-carrier ratios (y-axis) for vaccine serotypes (VT) and non-vaccine serotypes (NVT) before (panel A) and after vaccination (panel B). The incidences of disease (DVT and DNVT) are obtained by multiplication of the two quantities and correspond to the areas of the rectangles. After vaccination, VT carriage is eliminated and replaced by NVT carriage (panel B). The decrease in IPD incidence after vaccination is obtained as the difference between the eliminated VT disease and the replacing NVT disease. This is the area of the blue rectangle in panel B.]] | |||
'''Related research'''<br> | |||
The replacement model was built to reflect the accumulated 15 year long experience on use of pneumococcal conjugate vaccines worldwide and the related scientific research activity. Some of the most recent relevant publications are listed on a separate page: [[References]]. | |||
'''Sensitivity analysis'''<br> | |||
To assess the sensitivity of the predictions produced by the epidemiological model, | |||
effects of some alternative scenarios regarding the role of certain serotypes in PCV10 and PCV13 were calculated. | |||
In particular, these scenarios concern assumptions about indirect protection against serotype 3 under PCV13, | |||
indirect protection against serotype 6A under PCV10, and direct protection against 19A in PCV10. The detailed results are | |||
reported on a separate page: [[Sensitivity_analysis_pcv_model]]. In summary, the most influential assumptions are whether or not there will be population-level (indirect) impact on serotype 3 disease under PCV13 and serotype 6A disease under PCV10. | |||
=== Data === | |||
{{hidden| | |||
<t2b name='Pneumococcal carriage and IPD _' index='Serotype,Age,Observation' locations='Carriage,IPD' unit='Number of cases per year'> | |||
19F|Under 5|156030|7.78 | |||
23F|Under 5|156030|7.88 | |||
6B|Under 5|126990|24.39 | |||
14|Under 5|41200|20.76 | |||
9V|Under 5|22290|2.91 | |||
4|Under 5|12830|2.91 | |||
18C|Under 5|10130|6.64 | |||
1|Under 5|10|0.31 | |||
7|Under 5|14180|3.02 | |||
6A|Under 5|54940|3.94 | |||
19A|Under 5|24320|9.88 | |||
3|Under 5|12160|1.25 | |||
8|Under 5|1350|0.1 | |||
9N|Under 5|20940|0.83 | |||
10|Under 5|4050|0.41 | |||
11|Under 5|72270|0.42 | |||
12|Under 5|10|0.21 | |||
15|Under 5|33100|1.98 | |||
16|Under 5|3380|0.21 | |||
20|Under 5|1350|0.01 | |||
22|Under 5|12160|0.93 | |||
23A|Under 5|3380|0.1 | |||
33|Under 5|680|0.42 | |||
35|Under 5|30400|0.31 | |||
38|Under 5|4050|0.42 | |||
6C|Under 5|27470|0.01 | |||
Oth|Under 5|24320|0.73 | |||
19F|Over 5|168100|28.51 | |||
23F|Over 5|314800|53.72 | |||
6B|Over 5|256700|29.53 | |||
14|Over 5|209800|99.43 | |||
9V|Over 5|114100|43.07 | |||
4|Over 5|62500|76.99 | |||
18C|Over 5|200700|24.39 | |||
1|Over 5|100|6.58 | |||
7|Over 5|100|46.88 | |||
6A|Over 5|158800|17.42 | |||
19A|Over 5|54900|20.54 | |||
3|Over 5|30800|55.04 | |||
8|Over 5|8800|11.21 | |||
9N|Over 5|8800|25.2 | |||
10|Over 5|20800|6.28 | |||
11|Over 5|97700|12.76 | |||
12|Over 5|100|13.89 | |||
15|Over 5|100|9.18 | |||
16|Over 5|191900|4.73 | |||
20|Over 5|25200|3.29 | |||
22|Over 5|72500|29.03 | |||
23A|Over 5|22000|4.4 | |||
33|Over 5|100|5.64 | |||
35|Over 5|71300|12.41 | |||
38|Over 5|100|1.43 | |||
6C|Over 5|79400|5.5 | |||
Oth|Over 5|330100|11.2 | |||
</t2b> | |||
<t2b name="Serotypes in typical pneumococcal vaccines" index="Vaccine" obs="Serotype" unit="-"> | |||
PCV10|19F | |||
PCV10|23F | |||
PCV10|6B | |||
PCV10|14 | |||
PCV10|9V | |||
PCV10|4 | |||
PCV10|18C | |||
PCV10|1 | |||
PCV10|7 | |||
PCV13|19F | |||
PCV13|23F | |||
PCV13|6B | |||
PCV13|14 | |||
PCV13|9V | |||
PCV13|4 | |||
PCV13|18C | |||
PCV13|1 | |||
PCV13|7 | |||
PCV13|3 | |||
PCV13|6A | |||
PCV13|19A | |||
Existing serotypes|19F | |||
Existing serotypes|23F | |||
Existing serotypes|6B | |||
Existing serotypes|14 | |||
Existing serotypes|9V | |||
Existing serotypes|4 | |||
Existing serotypes|18C | |||
Existing serotypes|1 | |||
Existing serotypes|7 | |||
Existing serotypes|6A | |||
Existing serotypes|19A | |||
Existing serotypes|3 | |||
Existing serotypes|8 | |||
Existing serotypes|9N | |||
Existing serotypes|10 | |||
Existing serotypes|11 | |||
Existing serotypes|12 | |||
Existing serotypes|15 | |||
Existing serotypes|16 | |||
Existing serotypes|20 | |||
Existing serotypes|22 | |||
Existing serotypes|23A | |||
Existing serotypes|33 | |||
Existing serotypes|35 | |||
Existing serotypes|38 | |||
Existing serotypes|6C | |||
Existing serotypes|Oth | |||
</t2b> | |||
}} | |||
=== Initiate functions (only for developers) === | |||
<rcode name="initiate" label="Initiate functions" embed=1> | |||
library(OpasnetUtils) | |||
#S1.4. The R-functions | |||
############################################################################### | |||
## | |||
## R code for the core methods introduced in | |||
## Markku Nurhonen and Kari Auranen: | |||
## "Optimal serotype compositions for pneumococcal conjugate | |||
## vaccination under serotype replacement", | |||
## PLoS Computational Biology, 2014. | |||
## | |||
############################################################################### | |||
## List of arguments common to most functions: | |||
## | |||
## IPD = matrix of IPD incidences by age class (columns) and serotype (rows) | |||
## Car = corresponding matrix of carriage incidences | |||
## VT_rows = vector of the row numbers in matrices IPD and Car | |||
## corresponding to vaccine types (VT_rows=0 for no vaccination) | |||
## p = proportion of lost VT carriage which is replaced by NVT carriage | |||
## q = proportion of VT carriage lost either due to elimination or replacement | |||
## | |||
## This code includes 4 functions: | |||
## Vaccination, NextVT, OptimalSequence and OptimalVacc. | |||
## | |||
{{ | Vaccination<-function(IPD,Car,VT_rows,p,q) { | ||
## | |||
## Result: | |||
## A list of 2 matrices: IPD and carriage incidences | |||
## after vaccination (corresponding to matrices IPD and Car). | |||
## [Markku Nurhonen 2013] | |||
## | |||
if (VT_rows[1]>0) { | |||
IPD<-as.matrix(IPD); Car<-as.matrix(Car) | |||
# Post vaccination carriage incidences | |||
Car_Total<-t(matrix(apply(Car,2,sum),dim(Car)[2],dim(Car)[1])) | |||
Car2<-Car; Car2[VT_rows,]<-0 | |||
Car_NVT<-t(matrix(apply(Car2,2,sum),dim(Car2)[2],dim(Car2)[1])) | |||
Car_VT<-Car_Total-Car_NVT | |||
CarNew<-q*(1+p*Car_VT/Car_NVT)*Car2+(1-q)*Car | |||
# Post vaccination IPD incidences | |||
NVT_rows<-seq(dim(IPD)[1])[-1*VT_rows] | |||
# CCR=Case-to-carrier ratios | |||
CCR<-IPD/Car ; IPDNew<-0*IPD | |||
# Apply the equation appearing above | |||
# equation (1) in text for each serotype. | |||
# First term applies to NVTs. | |||
IPDNew[VT_rows,]<-(1-q)*IPD[VT_rows,] | |||
# Second term applies to NVTs. | |||
IPDNew[NVT_rows,]<-((Car_NVT+p*q*Car_VT)*(Car/Car_NVT)*CCR)[NVT_rows,] | |||
} | |||
else { | |||
IPDNew<-IPD; CarNew<-Car | |||
} | |||
list(IPDNew,CarNew) | |||
} | |||
[[ | NextVT<-function(IPD,Car,VT_rows,p) { | ||
## | |||
## Result: | |||
## A vector of decreases in IPD due to adding a serotype | |||
## to the vaccine. If VT_rows=0, initially no vaccination. | |||
## For row indexes incuded in VT_rows, the result is 0. | |||
## [Markku Nurhonen 2013] | |||
## | |||
IPD<-as.matrix(IPD); Car<-as.matrix(Car) | |||
## VaccMat = IPD and Car matrices after vaccination | |||
VaccMat<-Vaccination(IPD,Car,VT_rows,p,1) | |||
IPD<-VaccMat[[1]]; Car<-VaccMat[[2]] | |||
## Total_IPD,Total_Car = Matrices corresponding to | |||
## overall IPD and carriage in each age class. | |||
Total_IPD<-t(matrix(apply(IPD,2,sum),dim(IPD)[2],dim(IPD)[1])) | |||
Total_Car<-t(matrix(apply(Car,2,sum),dim(Car)[2],dim(Car)[1])) | |||
## Effect = decrease in IPD when one serotype is added to the vaccine. | |||
## See equation (3) in text. | |||
Effect<-(Total_IPD-IPD)*((IPD/(Total_IPD-IPD))-(p*Car/(Total_Car-Car))) | |||
## Special case when only one NVT remains. | |||
IPD_nonzero<-which(apply(IPD,1,sum)!=0) | |||
if (length(IPD_nonzero)==1) {Effect[IPD_nonzero,]<-IPD[IPD_nonzero,]} | |||
## Result is obtained after summation over age classes. | |||
apply(Effect,1,sum) | |||
} | |||
OptimalSequence<-function(IPD,Car,VT_rows,Excluded_rows,p,HowmanyAdded) { | |||
## | |||
## Starting from VTs indicated by the vector VT_rows | |||
## (VT_rows=0, for no vaccination) sequentially add new VTs | |||
## to the vaccine composition s.t. at each step the optimal | |||
## serotype (corresponding to largest decrease in IPD) is added. | |||
## | |||
## Excluded_rows = Vector of indexes of the rows in matrices | |||
## IPD and Car corresponding to serotypes that are not to | |||
## be included in a vaccine composition, e.g. a row | |||
## corresponding to a group of serotypes labelled "Other". | |||
## Enter Excluded_rows=0 for no excluded serotypes. | |||
## HowmanyAdded = number of VTs to be added. | |||
## | |||
## Result: | |||
## Matrix of dimension 2*HowmanyAdded with 1st row indicating | |||
## the row numbers of added serotypes in the order they appear | |||
## in the sequence. The 2nd row lists the decreases in IPD | |||
## due to addition of each type. [Markku Nurhonen 2013] | |||
## | |||
IPD<-as.matrix(IPD); Car<-as.matrix(Car) | |||
## First check the maximum possible number of added VTs. | |||
VT_howmany<-length(VT_rows) | |||
if (VT_rows[1]==0) {VT_howmany<-0} | |||
Excluded_howmany<-length(Excluded_rows) | |||
if (Excluded_rows[1]==0) {Excluded_howmany<-0} | |||
HowmanyAdded<-min(HowmanyAdded,dim(IPD)[1]-(VT_howmany+Excluded_howmany)) | |||
BestVTs<-BestEffects<-rep(0,HowmanyAdded) | |||
## Sequential procedure: at each step find the best additional VT. | |||
for (i in 1:HowmanyAdded) { | |||
## Effects = Decrease in IPD after addition of each serotype | |||
Effects<-NextVT(IPD,Car,VT_rows,p) | |||
## Set Effects for VTs and excluded types equal to small values | |||
## so that none of these will be selected as the next VT. | |||
minvalue<- -2*max(abs(Effects)) | |||
if (Excluded_howmany>0) {Effects[Excluded_rows]<-minvalue} | |||
if (VT_rows[1]>0) {Effects[VT_rows]<-minvalue} | |||
## BestVTs[i] = Index of serotype with maximum decrease in IPD. | |||
BestVTs[i]<-order(-1*Effects)[1] | |||
## BestEffects[i] = Decrese in IPD due to addition of BestVTs[i] | |||
## to the vaccine. | |||
BestEffects[i]<-Effects[BestVTs[i]] | |||
VT_rows<-c(VT_rows,BestVTs[i]) | |||
if (VT_rows[1]==0) {VT_rows<-VT_rows[-1]} | |||
VaccMat<-Vaccination(IPD,Car,VT_rows,p,1) | |||
IPD<-VaccMat[[1]]; Car<-VaccMat[[2]] | |||
} | |||
t(matrix(c(BestVTs,BestEffects),HowmanyAdded,2)) | |||
} | |||
OptimalVacc<-function(IPD,Car,VT_rows,p,q,HowmanyAdded) { | |||
## | |||
## Result: | |||
## A list of 3 elements: (1) Row numbers of serotypes in the optimal | |||
## vaccine composition (2)-(3) IPD and carriage incidences | |||
## by serotype and age class corresponding to the optimal | |||
## vaccine formed using the sequential procedure in the | |||
## function OptimalSequence. [Markku Nurhonen 2013] | |||
## | |||
Additional_VTs<-OptimalSequence(IPD,Car,VT_rows,p,HowmanyAdded)[1,] | |||
All_VTs<-c(VT_rows,Additional_VTs) | |||
if (All_VTs[1]==0) All_VTs<-All_VTs[-1] | |||
VaccMat<-Vaccination(IPD,Car,All_VTs,p,q) | |||
list(All_VTs,VaccMat[[1]],VaccMat[[2]]) | |||
} | |||
VacCar <- Ovariable("VacCar", | |||
dependencies = data.frame(Name = c( | |||
"IPD", # incidence of pneumococcus disease | |||
"Car", # number of carriers of pneumococcus | |||
"servac", # ovariable of serotypes in vaccine (1 for serotypes in a vaccine, otherwise result is 0) | |||
"p", # proportion of eliminated VT carriage that is replaced by NVT carriage | |||
"q" # proportion of of VT carriage eliminated by vaccine | |||
)), | |||
formula = function(...) { | |||
## Result: | |||
## An ovariable of carriage incidences | |||
## after vaccination (corresponding to Car). | |||
## [Markku Nurhonen 2013, Jouni Tuomisto 2014] | |||
# Post vaccination carriage incidences | |||
# Sum over serotypes and drop extra columns | |||
#Car_Total<- unkeep(oapply(Car, cols = "Serotype", FUN = sum) * 1, prevresults = TRUE) | |||
# Car2 is a temporary ovariable with NVT carriers only | |||
#Car2 <- unkeep(Car * (1 - servac), prevresults = TRUE) # Take only NVT carriers | |||
#Car_NVT <- oapply(Car2, cols = "Serotype", FUN = sum) # Carriers of serotypes not in vaccine (NVT) | |||
#Car_VT <- Car_Total - Car_NVT # Carriers of vaccine serotypes | |||
#CarNew <- q * (1 + p * Car_VT / Car_NVT) * Car2 + (1 - q) * Car | |||
eliminated <- q * servac * Car | |||
eliminated <- unkeep(eliminated, prevresults = TRUE) | |||
replaced <- oapply(eliminated, NULL, sum, "Serotype") * p | |||
# Distribute increase evenly among non-vaccine serotypes | |||
replaced <- unkeep(1 - servac, prevresults = TRUE) / | |||
oapply(unkeep(1 - servac, prevresults = TRUE), NULL, sum, "Serotype") * | |||
replaced | |||
replaced <- unkeep(replaced, prevresults = TRUE) | |||
CarNew <- Car - eliminated + replaced | |||
return(CarNew) | |||
} | |||
) | |||
VacIPD <- Ovariable("VacIPD", | |||
dependencies = data.frame(Name = c( | |||
"IPD", # incidence of pneumococcus disease | |||
"Car", # number of carriers of pneumococcus | |||
"servac", # ovariable of serotypes in vaccine (1 for serotypes in a vaccine, otherwise result is 0) | |||
"p", # proportion of eliminated VT carriage that is replaced by NVT carriage | |||
"q" # proportion of of VT carriage eliminated by vaccine | |||
#"VacCar" # proportional serotype carriage after vaccination | |||
)), | |||
formula = function(...) { | |||
## Result: | |||
## An ovariable of IPD incidence | |||
## after vaccination (corresponding to ovariable IPD). | |||
## [Markku Nurhonen 2013, Jouni Tuomisto 2014] | |||
# Post vaccination carriage incidences (same code as in VacCar) | |||
#Car_Total <- unkeep(oapply(Car, cols = "Serotype", FUN = sum) * 1, prevresults = TRUE) # Sums over serotypes | |||
#Car2 <- unkeep(Car * (1 - servac), prevresults = TRUE) | |||
#Car_NVT <- oapply(Car2, cols = "Serotype", FUN = sum) # Carriers of serotypes not in vaccine (NVT) | |||
#Car_VT <- Car_Total - Car_NVT # Carriers of vaccine serotypes | |||
#CarNew <- q * (1 + p * Car_VT / Car_NVT) * Car2 + (1 - q) * Car | |||
# Post vaccination IPD incidences | |||
# CCR=Case-to-carrier ratios | |||
#CCR <- IPD / Car | |||
# Apply the equation appearing above | |||
# equation (1) in text for each serotype. | |||
# First term applies to VTs. | |||
#IPDNewVT <- (1 - q) * IPD * servac | |||
# Second term applies to NVTs. | |||
#IPDNewNVT <- (Car_NVT + p * q * Car_VT) * (Car / Car_NVT) * CCR * (1 - servac) | |||
#IPDNew <- IPDNewVT + IPDNewNVT | |||
#IPDNew <- IPD * unkeep(VacCar, prevresults = TRUE) / Car | |||
#IPDNew <- IPD * exp(unkeep(log(VacCar), prevresults = TRUE) - unkeep(log(Car), prevresults = TRUE)) | |||
eliminated <- q * servac * Car | |||
eliminated <- unkeep(eliminated, prevresults = TRUE) | |||
replaced <- oapply(eliminated, NULL, sum, "Serotype") * p | |||
# Distribute increase evenly among non-vaccine serotypes | |||
#replaced <- unkeep(1 - servac, prevresults = TRUE) / | |||
# oapply(1 - servac, NULL, sum, "Serotype") * | |||
# replaced | |||
replaced <- unkeep(replaced, prevresults = TRUE) | |||
IPDNew <- ((1 - q * servac) + (1 - servac) * replaced / oapply((1 - servac) * Car, NULL, sum, "Serotype")) * IPD | |||
#oapply(IPDNew, IPDNew@output$Vaccine, sum) | |||
return(IPDNew) | |||
} | |||
) | |||
objects.store(Vaccination, NextVT, OptimalSequence, OptimalVacc, VacCar, VacIPD) | |||
cat("the functions Vaccination, NextVT, OptimalSequence, OptimalVacc and the ovariables VacCar, VacIPD are now saved. \n") | |||
</rcode> | |||
== See also == | |||
{{pneumococcal vaccine}} | |||
== References == | |||
<references/> | |||
== Related files == | |||
* {{#l:GSK 03 Epidemiological modelling_final_for Opasnet.docx}} | |||
== Comment the content == | |||
{{commenting tool}} | |||
Latest revision as of 11:21, 23 March 2016
| Moderator:Mnud (see all) |
|
|
| Upload data
|
In Opasnet many pages being worked on and are in different classes of progression. Thus the information on those pages should be regarded with consideration. The progression class of this page has been assessed:
|
The content and quality of this page is/was being curated by the project that produced the page.
The quality was last checked: 2016-03-21. |
Question
How to predict the net effectiveness of pneumococcal conjugate vaccination with a given set of serotypes when the vaccine is included in the national immunisation programme?
- The focus is on the incidence of invasive pneumococcal disease (IPD) cases in different age groups covering the whole population.
- The model is assumed to be valid in a population in which pneumococcal conjugate vaccination of infants has been in place for several years so that a new steady-state after vaccination has been reached.
- The coverage of vaccination and vaccine efficacy against carriage are assumed to be high enough to justify the assumption of complete elimination of vaccine-type carriage among both the vaccinated and also, due to substantial herd effects, among the unvaccinated members of the population.
- Vaccine-type carriage will be completely replaced by carriage of the non-vaccine types whose disease causing potential is not altered by vaccination.
Answer
The predicted reduction in the incidence of invasive pneumococcal disease (IPD) in different age groups are obtained from the serotype replacement model [1].
Computation
The following program illustrates the working of the replacement model. In its current implementation the code allows the user to specify upto 4 vaccine compositions and then displays the predicted number of IPD cases in Finland per year corresponding to these vaccines. The results are shown by serotype and by age category (<5 and 5+ year olds). Possible choices for vaccine compositions are: PCV10, PCV13, no vaccination and a user specified serotype composition. The program is based on the code in File S1 in [1].
- Instructions for user: Choose the desired vaccine compositions from the list below and then press "Run code".
You can compare 2,3 or 4 vaccine compositions. The results will be displayed on a separate tab. The default choice is PCV10 and PCV13.
Rationale
The epidemiological model for pneumococcal carriage and disease is based on the assumption that vaccination completely eliminates vaccine-type carriage in the vaccinated population and that vaccine-type carriage is completely replaced by non-vaccine-type carriage. The implications of this replacement on the decrease or increase in pneumococcal disease then depend on the disease causing potential of the replacing types compared to that of the replaced types. To predict the incidence of post-vaccination disease only pre-vaccination data on serotype-specific carriage and disease are used.
The consequences of serotype replacement in the model depend on two key assumptions regarding the new steady-state after vaccination:
- the relative serotype proportions among the non-vaccine types are not affected by vaccination (proportionality assumption);
- the case-to-carrier ratios (the disease causing potentials) of individual serotypes remain at their pre-vaccination levels.
The implications of vaccination on disease incidence are assumed to be solely due to the elimination of vaccine type carriage and its replacement by non vaccine-type carriage. An exception to this is when protective efficacy against disease without any efficacy against carriage is assumed for certain serotypes (a feature to be added).
Related research
The replacement model was built to reflect the accumulated 15 year long experience on use of pneumococcal conjugate vaccines worldwide and the related scientific research activity. Some of the most recent relevant publications are listed on a separate page: References.
Sensitivity analysis
To assess the sensitivity of the predictions produced by the epidemiological model,
effects of some alternative scenarios regarding the role of certain serotypes in PCV10 and PCV13 were calculated.
In particular, these scenarios concern assumptions about indirect protection against serotype 3 under PCV13,
indirect protection against serotype 6A under PCV10, and direct protection against 19A in PCV10. The detailed results are
reported on a separate page: Sensitivity_analysis_pcv_model. In summary, the most influential assumptions are whether or not there will be population-level (indirect) impact on serotype 3 disease under PCV13 and serotype 6A disease under PCV10.
Data
| Show details | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Initiate functions (only for developers)
See also
References
Related files
Comment the content