Probability theory and decision theory: Difference between revisions
No edit summary |
m (template added) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{encyclopedia}} | |||
This page about '''probability theory and decision theory''' will deal about Bayesian, that is, subjective probability, and its use in normative decision analysis. | This page about '''probability theory and decision theory''' will deal about Bayesian, that is, subjective probability, and its use in normative decision analysis. | ||
| Line 12: | Line 13: | ||
[[image:Operators and or in probability.PNG]] | [[image:Operators and or in probability.PNG]] | ||
Basic rules in probability | |||
The probability of A happening = p(A) | |||
p(A)+p(not A)=1 | |||
p(A or B) = p(A)+p(B)-p(A and B) | |||
:If A and B are mutually exclusive: p(A)+p(B) | |||
p(A|B) = p(A given B) = p(A and B)/p(B) | |||
p(A and B) = p(A|B)p(B) | |||
:If A and B not dependent (uncorrelated): p(A)p(B) | |||
| Line 78: | Line 96: | ||
u=utility, d=decision, i=individual | u=utility, d=decision, i=individual | ||
*Cost benetit analysis | |||
*Cost effectiveness analysis | |||
Latest revision as of 10:57, 3 October 2008
This page is a encyclopedia article.
The page identifier is Op_en1514 |
|---|
| Moderator:Nobody (see all) Click here to sign up. |
|
|
| Upload data
|
This page about probability theory and decision theory will deal about Bayesian, that is, subjective probability, and its use in normative decision analysis.
- Probability theory [frequentist and subjective (Bayesian) approach] Marja-Leenalla sopivia kirjoja? Uncertainty 220-230. Jouni
- Decision theory (utility, decision tree, utilitarian, egalitarian and other decision rules) Decision theory
Two approaches in probability
- Frequentist: Probability is the frequency distribution of outcomes, when a large number of similar events is repeated and obseverd, such tossing a coin, throwing a dice, or taking a blood test from a random sample of individuals in a population.
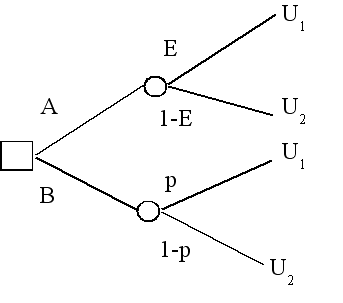
- Bayesian: When you are indifferent about choosing between A and B, your probability for U1 given A is E.
Basic rules in probability
The probability of A happening = p(A)
p(A)+p(not A)=1
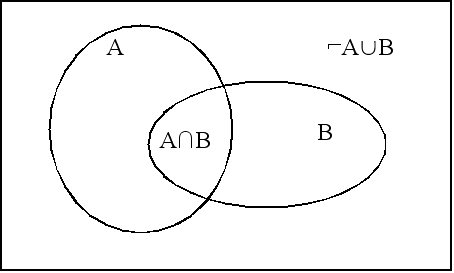
p(A or B) = p(A)+p(B)-p(A and B)
- If A and B are mutually exclusive: p(A)+p(B)
p(A|B) = p(A given B) = p(A and B)/p(B)
p(A and B) = p(A|B)p(B)
- If A and B not dependent (uncorrelated): p(A)p(B)
The probability of causation (POC)
POC = P(risk from the cause of interest)/P(risk due to all causes)
What is the POC for PM2.5 causing cardiovasular deaths in the EU?
What is the POC for vinylchloride causing angiosarcoma in liver?
POC(PM2.5 causing cardiovasular deaths in the EU):
350 000 deaths/a / 2 000 000 deaths/a = 0.175
"Internationally: Worldwide incidence also is low. Reports show angiosarcoma of the liver with an annual incidence of 2 cases per 10 million population, rising to 2.5 cases per 1000 population in workers exposed to vinyl chloride." [1]
POC(vinylchloride causing angiosarcoma in liver):
POC = (2.5*10-3 - 2*10-7)/(2.5*10-3) = 0.99992
Bayes' rule
(en:Risk aversion en:Risk premium)
Decision rules:
- Utilitarian: maxd(E(∑(ud,i)))
- Egalitarian: maxd(E(min(ud,i)))
- Elitist: maxd(E(max(ud,i)))
u=utility, d=decision, i=individual
- Cost benetit analysis
- Cost effectiveness analysis