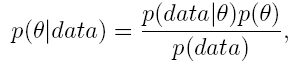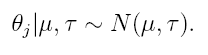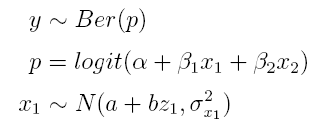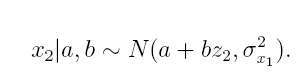Bayesian analysis: Difference between revisions
mNo edit summary |
(categorised) |
||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The text below is based on the review document | [[Category:Bayes]] | ||
[[Category:Intarese]] | |||
{{encyclopedia|moderator=Jouni}} | |||
The text below is based on the review document put together in the first phase of Intarese project. The original document can be found here: [[:intarese:Media:Bayes review.pdf|Bayes review]] | |||
Additional information on [http://en.wikipedia.org/wiki/Bayesian_probability Bayesian statistics] (note: external link to Wikipedia). | |||
KTL (M. Hujo) | KTL (M. Hujo) | ||
| Line 5: | Line 11: | ||
== Basic ideas == | == Basic ideas == | ||
Most researchers first meet with concepts of statistics through the | Most researchers first meet with concepts of statistics through the frequentist paradigm. | ||
Bayesian statistics offers us an alternative to | Bayesian statistics offers us an alternative to frequentist methods. | ||
Bayesian thinking and modeling is based on probability distributions. Very basic | Bayesian thinking and modeling is based on probability distributions. Very basic | ||
concepts in Bayesian analysis are prior and | concepts in Bayesian analysis are prior and posterior distributions. A prior distribution p(θ) summarizes our existing knowledge on θ (before data are seen). It can, | ||
for example, describe the opinion of a specialist and therefore Bayesian modelling requires that we accept the concept of subjective probability. A posterior distribution | for example, describe the opinion of a specialist and therefore Bayesian modelling requires that we accept the concept of subjective probability. A posterior distribution | ||
p(θ|data) describes our updated knowledge after we have seen data. A posterior is | p(θ|data) describes our updated knowledge after we have seen data. A posterior is | ||
formed by combining a prior and likelihood p(data|θ) (derived using the same techniques | formed by combining a prior and likelihood p(data|θ) (derived using the same techniques | ||
as in | as in frequentist statistics) using Bayes' formula, | ||
<center> | <center> | ||
[[Image:Bayes formula.PNG]] | |||
</center> | |||
As we can see, this is a natural mechanism for learning | As we can see, this is a natural mechanism for learning; it gives a direct answer to the | ||
question: "How | question: "How do data change our belief in the matter we are studying?" | ||
From above we also see that one of the main differences between frequentist | From the above we can also see that one of the main differences between frequentist | ||
and Bayesian analyses lies in whether we use only | and Bayesian analyses lies in whether we use only likelihoods or whether we also | ||
use prior | use prior distributions. The prior distribution allows us to make use of information from | ||
earlier studies. We summarize this information with our prior distribution and then | earlier studies. We summarize this information with our prior distribution and then | ||
use Bayes' formula and our own data to update our knowledge. If we do not have | use Bayes' formula and our own data to update our knowledge. If we do not have | ||
any previous information on the issue we are studying we may use so called uninformative | any previous information on the issue we are studying we may use the so-called uninformative | ||
prior meaning that our prior distribution does not contain much information, for | prior meaning that our prior distribution does not contain much information, for | ||
example a normal distribution with large variance. As we see from Bayes' formula, the use | example a normal distribution with a large variance. As we see from Bayes' formula, the use | ||
of uninformative prior lets data define our posterior distribution. | of the uninformative prior lets data define our posterior distribution. | ||
Of course there are also differences between Bayesian and frequentistic statistics. | Of course there are also differences between Bayesian and frequentistic statistics. | ||
One is the way of thinking. In frequentistic analysis the parameter θ is taken to be fixed | One of these differences is the ''way'' of thinking. In frequentistic analysis the parameter θ is taken to be fixed | ||
(albeit unknown) and data is considered to be random whereas Bayesian statisticians | (albeit unknown) and data is considered to be random, whereas Bayesian statisticians | ||
would say that θ is uncertain and follows a probability distribution while data is taken to | would say that θ is uncertain and follows a probability distribution while data is taken to | ||
be fixed. | be fixed. | ||
It is important to note that Bayesian analysis carefully distinguishes between p(θ | data) and p(data | θ) and all inference from Bayesian analysis is based on a | |||
posterior distribution, which is a true probability distribution. Thus Baysian | posterior distribution, which is a true probability distribution. Thus Baysian analysis ensures natural intepretations for our estimators and probability intervals. More | ||
on the basics of Bayesian analysis can be found for example in [1] and [2]. | on the basics of Bayesian analysis can be found for example in [1] and [2]. | ||
| Line 44: | Line 51: | ||
In practice it is not straightforward to compute an arbitrary posterior distribution, | In practice it is not straightforward to compute an arbitrary posterior distribution, | ||
but we can sample from it. For sampling we may use the Markov chain Monte Carlo | but we can sample from it. For sampling we may use the Markov chain Monte Carlo (MCMC) | ||
concept. In simple terms, the idea is to construct a Markov | |||
chain such that it has the desired posterior distribution as its limiting distribution. Then | chain such that it has the desired posterior distribution as its limiting distribution. Then | ||
we simulate this chain and get a sample from the desired distribution. Perhaps the most commonly | we simulate this chain and get a sample from the desired distribution. Perhaps the most commonly | ||
| Line 63: | Line 70: | ||
in which for each center there is a center-specific "true effect" included. | in which for each center there is a center-specific "true effect" included. | ||
Bayesian methods allow us to deal with these problems within a unified | Bayesian methods allow us to deal with these problems within a unified | ||
framework (cf. [5]). A major advantage in the Bayesian approach is the ease with | |||
which one can include study-specific covariates and that inference concerning the | which one can include study-specific covariates and that inference concerning the | ||
study-specific effects is done a natural manner through the posterior distributions. | study-specific effects is done a natural manner through the posterior distributions. | ||
Compared to classical methods Bayesian approach | Compared to classical methods, the Bayesian approach potentially gives a more complete | ||
representation of between-study heterogeneity and | representation of between-study heterogeneity and a more transparent and | ||
intuitive reporting of results. Of course the cost of these benefits is that a prior | intuitive reporting of results. Of course the cost of these benefits is that a prior | ||
specification is required. | specification is required. | ||
| Line 77: | Line 84: | ||
normally distributed i.e. | normally distributed i.e. | ||
<center> | <center> | ||
[[Image:Normal point estimators.PNG]] | |||
</center> | |||
We can simplify this model by assuming that σ<sub>j</sub> is known. This simplification does | We can simplify this model by assuming that σ<sub>j</sub> is known. This simplification does | ||
not have much effect if sample sizes for each study are large enough. As an estimator | not have much effect if sample sizes for each study are large enough. As an estimator | ||
of σ<sub>j</sub> we can take for example sampling variance of point estimator y<sub>j</sub>. | of σ<sub>j</sub> we can take for example the sampling variance of a point estimator y<sub>j</sub>. | ||
The second stage of our model assumes normality for θ<sub>j</sub> conditioned on hyperparameters μ ja τ , | The second stage of our model assumes normality for θ<sub>j</sub> conditioned on hyperparameters μ ja τ , | ||
<center> | <center> | ||
[[Image:Hyperparameters.PNG]] | |||
</center> | |||
Finally, we assume noninformative hyperpriors for μ and τ . The analysis of our | Finally, we assume noninformative hyperpriors for μ and τ . The analysis of our | ||
| Line 95: | Line 106: | ||
== Combining information from different types of studies == | == Combining information from different types of studies == | ||
Let us now consider an example on air pollution (fine particles) and its | Let us now consider an example on air pollution (fine particles) and its health effects | ||
measured by | measured by health test. We are interested in the relationship of personal exposure to fine particulate | ||
matter and the health effect. For | matter and the associated health effect. For health effect we have binary data y, y ~ Ber(p), | ||
given by a health test (st depression) where one indicates a health problem and zero | given by a health test (st depression) where one indicates a health problem and zero | ||
stands for no problem. We also have data on ambient concentration of fine particle | stands for no problem. We also have data on the ambient concentration of the fine particle | ||
matter, denoted by variable z<sub>1</sub>, for each day of health test. What we do not have | matter, denoted by variable z<sub>1</sub>, for each day of the health test. What we do not have are | ||
data on personal exposure for health measurement days which we denote by x<sub>1</sub>. So | data on personal exposure for health measurement days, which we denote by x<sub>1</sub>. So | ||
there is a missing information between personal exposure and | there is a missing piece of information between personal exposure and the health test. However, | ||
we have another data set that connects ambient concentration to personal exposure. | we do have another data set that connects ambient concentration to personal exposure. | ||
In this second data set we denote ambient concentration by z<sub>2</sub> and personal exposure | In this second data set we denote ambient concentration by z<sub>2</sub> and personal exposure | ||
by x<sub>2</sub>. | by x<sub>2</sub>. The solution to our problem now is a model consisting of two parts. First part is | ||
logistic | logistic health effect model which assumes that | ||
<center> | <center>[[Image:Logistic health effect model.PNG]]</center> | ||
where c stands for all confounding variables required in model. | where c stands for all confounding variables required in model. The second part is a | ||
linear regression model | linear regression model | ||
<center> | <center>[[Image:Linear regression.PNG]]</center> | ||
| Line 123: | Line 134: | ||
<center> | <center>[[Image:Params a and b.PNG]]</center> | ||
using our second data set. One of | using our second data set. One of the advantages of using Bayesian statistics here to analyze | ||
the relationship between personal exposure and a health effect is that the model takes into account | |||
our uncertainty of x<sub>1</sub> in (1.1). | our uncertainty of x<sub>1</sub> in (1.1). | ||
To summarize above we have | To summarize the above we have | ||
<center> | <center> | ||
[[Image:To summarize.PNG]] | |||
[[Image:To summarize 2.PNG]] | |||
</center> | |||
To complete our model we set some prior distributions for parameters ά, β<sub>1</sub>, β<sub>2</sub> | To complete our model we set some prior distributions for parameters ά, β<sub>1</sub>, β<sub>2</sub> | ||
and for parameters a and b. The posterior distribution of this model can be simulated | and for parameters a and b. The posterior distribution of this model can be simulated | ||
using MCMC methods described above. This kind of idea is applied for example in [3]. | using the MCMC methods described above. This kind of idea is applied for example in [3]. | ||
== Final remarks == | == Final remarks == | ||
| Line 156: | Line 161: | ||
estimators and probability intervals are very natural because Bayesian analysis | estimators and probability intervals are very natural because Bayesian analysis | ||
is based on true probability distributions. For example a Bayesian 95% probability | is based on true probability distributions. For example a Bayesian 95% probability | ||
interval | interval should be interpreted such that a parameter of interest µ lies in that interval with | ||
probability 0 | a probability of 0.95. A frequentistic confidence interval is a random interval meaning that | ||
if we would repeat our calculations 100 times with new data each time then, | if we would repeat our calculations 100 times with new data each time then, on | ||
average, 95 of our confidence intervals would contain θ. | average, 95 of our confidence intervals would contain θ. | ||
| Line 173: | Line 178: | ||
[5] T. Smith, D. Spiegelhalter, A. Thomas Bayesian approaches to random-effects | [5] T. Smith, D. Spiegelhalter, A. Thomas Bayesian approaches to random-effects | ||
meta-analysis: a comparative study. Statistics in Medicine (1995) 14(24) pp. 2685-99. | meta-analysis: a comparative study. Statistics in Medicine (1995) 14(24) pp. 2685-99. | ||
Latest revision as of 13:30, 15 January 2010
| [show] This page is a encyclopedia article.
The page identifier is Op_en3792 |
|---|
The text below is based on the review document put together in the first phase of Intarese project. The original document can be found here: Bayes review
Additional information on Bayesian statistics (note: external link to Wikipedia).
KTL (M. Hujo)
Basic ideas
Most researchers first meet with concepts of statistics through the frequentist paradigm. Bayesian statistics offers us an alternative to frequentist methods.
Bayesian thinking and modeling is based on probability distributions. Very basic concepts in Bayesian analysis are prior and posterior distributions. A prior distribution p(θ) summarizes our existing knowledge on θ (before data are seen). It can, for example, describe the opinion of a specialist and therefore Bayesian modelling requires that we accept the concept of subjective probability. A posterior distribution p(θ|data) describes our updated knowledge after we have seen data. A posterior is formed by combining a prior and likelihood p(data|θ) (derived using the same techniques as in frequentist statistics) using Bayes' formula,
As we can see, this is a natural mechanism for learning; it gives a direct answer to the question: "How do data change our belief in the matter we are studying?"
From the above we can also see that one of the main differences between frequentist and Bayesian analyses lies in whether we use only likelihoods or whether we also use prior distributions. The prior distribution allows us to make use of information from earlier studies. We summarize this information with our prior distribution and then use Bayes' formula and our own data to update our knowledge. If we do not have any previous information on the issue we are studying we may use the so-called uninformative prior meaning that our prior distribution does not contain much information, for example a normal distribution with a large variance. As we see from Bayes' formula, the use of the uninformative prior lets data define our posterior distribution.
Of course there are also differences between Bayesian and frequentistic statistics. One of these differences is the way of thinking. In frequentistic analysis the parameter θ is taken to be fixed (albeit unknown) and data is considered to be random, whereas Bayesian statisticians would say that θ is uncertain and follows a probability distribution while data is taken to be fixed.
It is important to note that Bayesian analysis carefully distinguishes between p(θ | data) and p(data | θ) and all inference from Bayesian analysis is based on a posterior distribution, which is a true probability distribution. Thus Baysian analysis ensures natural intepretations for our estimators and probability intervals. More on the basics of Bayesian analysis can be found for example in [1] and [2].
Markov chain Monte Carlo
In practice it is not straightforward to compute an arbitrary posterior distribution, but we can sample from it. For sampling we may use the Markov chain Monte Carlo (MCMC) concept. In simple terms, the idea is to construct a Markov chain such that it has the desired posterior distribution as its limiting distribution. Then we simulate this chain and get a sample from the desired distribution. Perhaps the most commonly used software writen for MCMC is called BUGS which is an abbreviation of 'Bayesian statistics Using Gibbs Sampling'.
Bayesian meta-analysis
A meta-analysis is a statistical procedure in which the results of several independent studies are integrated. There are always some basic issues to be considered in meta- analysis such as the choice between using a fixed-effects model or a random-effects model, the treament of small studies and incorporation of study-specific covariates. For example, analysis of the results of a clinical trial with many health care centers involved. The centers may differ in their patient pool e.g. number of patients, overall health level and age or the quality of the health care they provide. It is widely recognized that it is important to explicitly deal with the heterogeneity of the studies through random-effects models, in which for each center there is a center-specific "true effect" included. Bayesian methods allow us to deal with these problems within a unified framework (cf. [5]). A major advantage in the Bayesian approach is the ease with which one can include study-specific covariates and that inference concerning the study-specific effects is done a natural manner through the posterior distributions. Compared to classical methods, the Bayesian approach potentially gives a more complete representation of between-study heterogeneity and a more transparent and intuitive reporting of results. Of course the cost of these benefits is that a prior specification is required.
To shed more light on Bayesian meta-analysis, let us now give a relatively simple example. Assume that we have n studies. We are interested in average µ of the parameters θj , j = 1,..,n. Using information available from these studies we calculate a point estimator yj for parameter θj . The first stage of the hierarchical Bayesian model assumes that the point estimators conditioned on parameters are e.g. normally distributed i.e.
We can simplify this model by assuming that σj is known. This simplification does not have much effect if sample sizes for each study are large enough. As an estimator of σj we can take for example the sampling variance of a point estimator yj.
The second stage of our model assumes normality for θj conditioned on hyperparameters μ ja τ ,
Finally, we assume noninformative hyperpriors for μ and τ . The analysis of our meta-analysis model follows a now normal Bayesian procedure, the inference is again based on posterior distribution p(μ | data).
More reading on the applications of Bayesian meta-analysis can be found in [3] and [4].
Combining information from different types of studies
Let us now consider an example on air pollution (fine particles) and its health effects measured by health test. We are interested in the relationship of personal exposure to fine particulate matter and the associated health effect. For health effect we have binary data y, y ~ Ber(p), given by a health test (st depression) where one indicates a health problem and zero stands for no problem. We also have data on the ambient concentration of the fine particle matter, denoted by variable z1, for each day of the health test. What we do not have are data on personal exposure for health measurement days, which we denote by x1. So there is a missing piece of information between personal exposure and the health test. However, we do have another data set that connects ambient concentration to personal exposure. In this second data set we denote ambient concentration by z2 and personal exposure by x2. The solution to our problem now is a model consisting of two parts. First part is logistic health effect model which assumes that
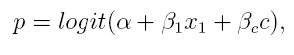
where c stands for all confounding variables required in model. The second part is a
linear regression model
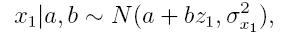
where we obtain estimates to personal exposure on health test days. Parameters a
and b are estimated from
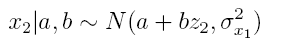
using our second data set. One of the advantages of using Bayesian statistics here to analyze
the relationship between personal exposure and a health effect is that the model takes into account
our uncertainty of x1 in (1.1).
To summarize the above we have
To complete our model we set some prior distributions for parameters ά, β1, β2
and for parameters a and b. The posterior distribution of this model can be simulated
using the MCMC methods described above. This kind of idea is applied for example in [3].
Final remarks
Bayesian methods offer a rather flexible tool to combine studies and there is some software available to use with Bayesian analysis. Intepretations for Bayesian estimators and probability intervals are very natural because Bayesian analysis is based on true probability distributions. For example a Bayesian 95% probability interval should be interpreted such that a parameter of interest µ lies in that interval with a probability of 0.95. A frequentistic confidence interval is a random interval meaning that if we would repeat our calculations 100 times with new data each time then, on average, 95 of our confidence intervals would contain θ.
References
[1] P. Congdon. Applied Bayesian Modelling. Wiley series in probability and statistics 2003.
[2] A. Gelman, J. B. Carlin, H. S. Stern, D.B. Rubin. Bayesian data analysis. Chap-
man & Hall 2004.
[3] F. Dominici, J. M. Samet, S. L. Zeger A measurement error model for time-series
studies of air pollution and mortality. Biostatistics (2000), 1, pp. 157-175
[4] J. M. Samet, F. Dominici, F. C. Curriero, I. Coursac, S. L. Zeger. Fine partuculate
air pollution and mortality in 20 U.S. cities. The New Enland Journal of Medicine
(2000), 342, 24, pp. 1742-1749
[5] T. Smith, D. Spiegelhalter, A. Thomas Bayesian approaches to random-effects
meta-analysis: a comparative study. Statistics in Medicine (1995) 14(24) pp. 2685-99.